题目内容
已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
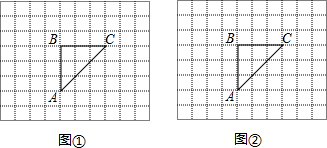
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
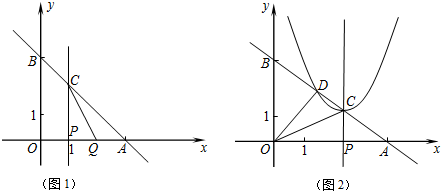
(2)当k=-
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),求CD的长.

(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=-
| 3 |
| 4 |
考点:二次函数综合题
专题:
分析:(1)①由题意可得P(t,0),C(t,-t+3),Q(3-t,0)代入t的数值得出答案即可;
②由题意得到关于t的坐标.按照两种情形解答,从而得到答案.
(2)以点C为顶点的抛物线,解得关于t的根,又由过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,又由△DEC∽△AOB从而解得.
②由题意得到关于t的坐标.按照两种情形解答,从而得到答案.
(2)以点C为顶点的抛物线,解得关于t的根,又由过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,又由△DEC∽△AOB从而解得.
解答:解:(1)①C(1,2),Q(2,0)
②由题意得:P(t,0),C(t,-t+3),Q(3-t,0).
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,
∴CQ⊥OA,
∵CP⊥OA,
∴点P与点Q重合,OQ=OP,
即3-t=t,
∴t=1.5;
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,
∵OA=OB=3,
∴△AOB是等腰直角三角形,
∴△ACQ也是等腰直角三角形.
∵CP⊥OA,
∴AQ=2CP,
即t=2(-t+3),
∴t=2.
∴满足条件的t的值是1.5秒或2秒;
(2)由题意得:C(t,-
t+3),
∴以C为顶点的抛物线解析式是y=(x-t)2-
t+3
由(x-t)2-
t+3=-
x+3,
∴(x-t)(x-t+
)=0,
解得x1=t,x2=t-
.
过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,

∵DE∥OA,
∴∠EDC=∠OAB,
∴△DEC∽△AOB,
∴
=
∵AO=4,AB=5,DE=t-(t-
)=
,
∴CD=
=
=
.
②由题意得:P(t,0),C(t,-t+3),Q(3-t,0).
分两种情况讨论:
情形一:当△AQC∽△AOB时,∠AQC=∠AOB=90°,
∴CQ⊥OA,
∵CP⊥OA,
∴点P与点Q重合,OQ=OP,
即3-t=t,
∴t=1.5;
情形二:当△ACQ∽△AOB时,∠ACQ=∠AOB=90°,
∵OA=OB=3,
∴△AOB是等腰直角三角形,
∴△ACQ也是等腰直角三角形.
∵CP⊥OA,
∴AQ=2CP,
即t=2(-t+3),
∴t=2.
∴满足条件的t的值是1.5秒或2秒;
(2)由题意得:C(t,-
| 3 |
| 4 |
∴以C为顶点的抛物线解析式是y=(x-t)2-
| 3 |
| 4 |
由(x-t)2-
| 3 |
| 4 |
| 3 |
| 4 |
∴(x-t)(x-t+
| 3 |
| 4 |
解得x1=t,x2=t-
| 3 |
| 4 |
过点D作DE⊥CP于点E,则∠DEC=∠AOB=90°,

∵DE∥OA,
∴∠EDC=∠OAB,
∴△DEC∽△AOB,
∴
| DE |
| AO |
| CD |
| BA |
∵AO=4,AB=5,DE=t-(t-
| 3 |
| 4 |
| 3 |
| 4 |
∴CD=
| DE•BA |
| AO |
| ||
| 4 |
| 15 |
| 16 |
点评:本题考查了二次函数的综合运用,以及相似三角形的判定与性质等知识,根据已知得出相似三角形进而得出线段长度是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算正确的是( )
| A、3a2-a=2a |
| B、(-a3)2=a5 |
| C、a6÷a4=a2 |
| D、(a-b)2=a2-b2 |
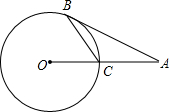 如图,AB与⊙O相切于点B,AO的连线交⊙O于点C;若∠A=50°,则∠ABC为
如图,AB与⊙O相切于点B,AO的连线交⊙O于点C;若∠A=50°,则∠ABC为 如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG. 如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=
如图:已知正方形OABC的边OC、OA分别在x轴和y轴的正半轴上,点B坐标为(4,4).二次函数y=