题目内容
我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.商家同时购进甲、乙两种商品共100件,设其中甲商品购进x件,售完此两种商品总利润为y元.
(1)写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
(1)写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
考点:一次函数的应用
专题:
分析:(1)根据总利润=甲种商品的利润+乙种商品的利润,由销售问题的数量关系就可以表示出y与x的函数关系式;
(2)根据两种商品的进价表示出甲乙两种商品的进价之和不超过3000建立不等式求出x的值,由一次函数的解析式的性质就可以求出结论.
(2)根据两种商品的进价表示出甲乙两种商品的进价之和不超过3000建立不等式求出x的值,由一次函数的解析式的性质就可以求出结论.
解答:解:(1)设其中甲商品购进x件,则乙商品进(100-x)件,由题意,得售完此两种商品总利润为y元
y=(20-15)x+(45-35)(100-x)=-5x+1000.
∴y与x之间的函数关系式为:y=-5x+1000;
(2)由题意,得
15x+35(100-x)≤3000,
解得:x≥25.
∵y=-5x+1000,
∴k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y最大,y最大=-5×25+1000=875.
∴最少购进25件甲种商品;可获得最大利润875元.
y=(20-15)x+(45-35)(100-x)=-5x+1000.
∴y与x之间的函数关系式为:y=-5x+1000;
(2)由题意,得
15x+35(100-x)≤3000,
解得:x≥25.
∵y=-5x+1000,
∴k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y最大,y最大=-5×25+1000=875.
∴最少购进25件甲种商品;可获得最大利润875元.
点评:本题考查了销售问题的数量关系的运用,一次函数的解析式的运用,一元一次不等式的运用,解答时运用销售问题的数量关系求出一次函数的解析式是关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
下列实数中,属于无理数的是( )
A、
| |||
B、
| |||
| C、π | |||
| D、3.3030030003 |
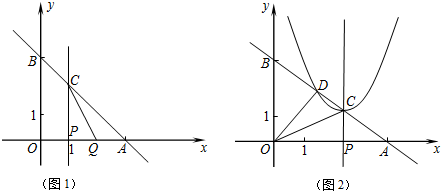
 如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=