题目内容
6.若A(-5,y1),B(-2,y2),C(1,y3)为二次函数y=ax2+2ax+2016(a<0)的图象上的三点,则y1,y2,y3的大小关系是( )| A. | y1<y3<y2 | B. | y2<y3<y1 | C. | y1<y2<y3 | D. | y3<y1<y2 |
分析 先由a<0,得出函数有最大值,再根据点A、B、C到对称轴的距离的大小与抛物线的增减性解答.
解答 解:二次函数y=ax2+2ax+2016的对称轴为直线x=-$\frac{2a}{2a}$=-1,
∵a<0,
∴抛物线开口向下,
∵点A、B、C到对称轴的距离分别为4、1、2,
∴y1<y3<y2.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,以及对称轴的求法,函数的增减性,掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
1.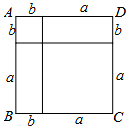 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
 如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )
如图,根据计算正方形ABCD的面积,可以说明下列哪个等式成立( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a+b)(a-b)=a2-b2 | D. | a(a-b)=a2-ab |
18.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )


| A. | 2016个 | B. | 2015个 | C. | 2014个 | D. | 2013个 |
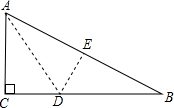 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则AD=3$\sqrt{5}$cm. 如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为60°.
如图,若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合,则α的最小值为60°.