题目内容
8.已知点M(-3,0),点N是点M关于原点的对称点,点A是函数y=-x+3$\sqrt{2}$图象上的一点,若△AMN是直角三角形,则点A的坐标为( )| A. | (3,3$\sqrt{2}$)或(-3,3+3$\sqrt{2}$) | B. | (-3,3+3$\sqrt{2}$)或(3,3$\sqrt{2}$)或($\frac{3}{2}$$\sqrt{2}$,$\frac{3}{2}$$\sqrt{2}$) | ||
| C. | (-3,3+3$\sqrt{2}$)或(3,3$\sqrt{2}$-3)或($\sqrt{2}$,2$\sqrt{2}$) | D. | (-3,3+3$\sqrt{2}$)或(3,3$\sqrt{2}$-3)或($\frac{3}{2}$$\sqrt{2}$,$\frac{3}{2}$$\sqrt{2}$) |
分析 分别过点M、N作x轴垂线与直线交点即为所求,由M、N点坐标可得点A坐标;在直线上取一点(x,-x+3$\sqrt{2}$),根据AM2+AN2=MN2列出关于x的方程,解方程可得第三个点A的坐标.
解答 解:①如图,过点M(-3,0)作x轴垂线交直线y=-x+3$\sqrt{2}$于点A1,则A1的坐标为(-3,3+3$\sqrt{2}$);
②过点N(3,0)作x轴垂线交直线y=-x+3$\sqrt{2}$于点A2,则A2的坐标为(3,-3+3$\sqrt{2}$);
③设直线y=-x+3$\sqrt{2}$上的点A3坐标为(x,-x+3$\sqrt{2}$),
根据题意,A3M2+A3N2=MN2,即(-3-x)2+(x-3$\sqrt{2}$)2+(3-x)2+(x-3$\sqrt{2}$)2=62,
整理,得:2x2-6$\sqrt{2}$x-9=0,
解得:x=$\frac{3}{2}$$\sqrt{2}$,
当x=$\frac{3}{2}$$\sqrt{2}$时,y=-$\frac{3}{2}$$\sqrt{2}$+3$\sqrt{2}$=$\frac{3}{2}$$\sqrt{2}$,
∴点A3的坐标为($\frac{3}{2}$$\sqrt{2}$,$\frac{3}{2}$$\sqrt{2}$),
综上,点A的坐标为(-3,3+3$\sqrt{2}$)、(3,-3+3$\sqrt{2}$)、($\frac{3}{2}$$\sqrt{2}$,$\frac{3}{2}$$\sqrt{2}$),
故选:D.
点评 本题主要考查一次函数图象上点的坐标、两点间距离公式、勾股定理,根据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
19.若$\sqrt{\frac{{x}^{2}}{4{y}^{2}}}$=-$\frac{x}{2y}$成立,则x、y符合的条件是( )
| A. | x≤0,y≠0 | B. | x≤0,y为一切实数 | C. | x<0,y≠0 | D. | 以上都不对 |
13. 如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
 如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )
如图,在矩形ABCD中,连接BD,将△ABD沿BD进行折叠,使得点A落到点M处,DM交BC于点N,若AB=2,BD=5,则MN的长度为( )| A. | $\frac{17\sqrt{21}}{42}$ | B. | $\frac{17\sqrt{21}}{21}$ | C. | 17$\sqrt{21}$ | D. | 34$\sqrt{21}$ |
20. 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
(3)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,当四边形OMAB为正方形时,a=2,m=$\frac{1}{2}$.
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.(1)试说明a=2时,四边形OMAB是菱形.
(2)当a的值分别取1,2,3时,分别计算s的值,将其填入如表
| a | 1 | 2 | 3 |
| s |
(4)将抛物线y=ax(x-2)(0<a<4)改为抛物线y=ax(x-2m)(0<a<4),其他条件不变,s=4m3(用含m的代数式表示)
 如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是40°.
如图,AB是⊙O的直径,点C,D都在⊙O上,∠ABC=50°,则∠BDC的大小是40°.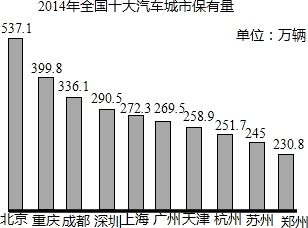 2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.
2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆. 如图,四边形ABCD是矩形,E、F分别是AB、CD的中点,现将矩形的一角沿过点B的折痕BM对折,使得点A落在线段EF上,记为N,则:
如图,四边形ABCD是矩形,E、F分别是AB、CD的中点,现将矩形的一角沿过点B的折痕BM对折,使得点A落在线段EF上,记为N,则: 关于x的一元二次方程a2x2+2ax-3=0(a≠0).
关于x的一元二次方程a2x2+2ax-3=0(a≠0).