题目内容
19．若$\sqrt{\frac{{x}^{2}}{4{y}^{2}}}$=-$\frac{x}{2y}$成立，则x、y符合的条件是（ ）| A． | x≤0，y≠0 | B． | x≤0，y为一切实数 | C． | x＜0，y≠0 | D． | 以上都不对 |
分析 首先把二次根式的被开方数化为平方的形式，再进一步观察被开方数与开方结果的联系，利用二次根式的性质得出答案即可．
解答 解：∵$\sqrt{\frac{{x}^{2}}{4{y}^{2}}}$=$\sqrt{（\frac{x}{2y}）^{2}}$=-$\frac{x}{2y}$，
∴xy≤0，且y≠0，
故选：D．
点评 此题考查利用二次根式的性质化简，注意被开方数与开方结果之间的联系．
练习册系列答案
相关题目
1．已知不等式组$\left\{\begin{array}{l}{x＞a}\\{x≥1}\end{array}\right.$的解集是x≥1，则a的取值范围是（ ）
| A． | a＜1 | B． | a≤1 | C． | a≥1 | D． | a＞1 |
2．
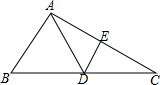如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，△ABC的周长为23，则△ABD的周长为（ ）
如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，△ABC的周长为23，则△ABD的周长为（ ）| A． | 13 | B． | 15 | C． | 17 | D． | 19 |
7．在数$\frac{22}{7}$，0，$\frac{π}{2}$，-1.414中，有理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．下列说法正确的是（ ）
| A． | 平行四边形是轴对称图形 | |
| B． | 平行四边形的对角线互相垂直平分 | |
| C． | 一组对边平行，另一组对边相等的四边形是平行四边形 | |
| D． | 两组对角分别相等的四边形是平行四边形 |
11．
甲乙都从A地出发到达B地，甲先出发0.6小时．如图所示描述两人的路程和时间的函数关系，下列说法正确的个数为（ ）
①乙在1.4小时后改变速度；
②甲乙两次相遇间隔为2小时；
③行驶完全程，乙比甲多用了2.4小时；
④两人的平均速度差为3.75千米/时．
甲乙都从A地出发到达B地，甲先出发0.6小时．如图所示描述两人的路程和时间的函数关系，下列说法正确的个数为（ ）①乙在1.4小时后改变速度；
②甲乙两次相遇间隔为2小时；
③行驶完全程，乙比甲多用了2.4小时；
④两人的平均速度差为3.75千米/时．
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
8．已知点M（-3，0），点N是点M关于原点的对称点，点A是函数y=-x+3$\sqrt{2}$图象上的一点，若△AMN是直角三角形，则点A的坐标为（ ）
| A． | （3，3$\sqrt{2}$）或（-3，3+3$\sqrt{2}$） | B． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$）或（$\frac{3}{2}$$\sqrt{2}$，$\frac{3}{2}$$\sqrt{2}$） | ||
| C． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$-3）或（$\sqrt{2}$，2$\sqrt{2}$） | D． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$-3）或（$\frac{3}{2}$$\sqrt{2}$，$\frac{3}{2}$$\sqrt{2}$） |
