题目内容
10．
如图，AB是⊙O的直径，点C，D都在⊙O上，∠ABC=50°，则∠BDC的大小是40°．
分析 根据∠ABC=50°求出$\widehat{ADC}$的度数为100°，求出$\widehat{BC}$的度数为80°，即可求出答案．
解答 解：∵∠ABC=50°，
∴$\widehat{ADC}$的度数为100°，
∵AB为直径，
∴$\widehat{BC}$的度数为80°，
∴∠BDC=$\frac{1}{2}$×80°=40°，
故答案为：40°．
点评 本题考查了圆周角定理的应用，能灵活运用定理求出$\widehat{BC}$的度数是解此题的关键，注意：在同圆中，圆周角的度数等于它所对的弧的度数的一半．
练习册系列答案
相关题目
20．计算：2$\sqrt{2}$-$\sqrt{2}$=（ ）
| A． | 3$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 1 |
1．已知不等式组$\left\{\begin{array}{l}{x＞a}\\{x≥1}\end{array}\right.$的解集是x≥1，则a的取值范围是（ ）
| A． | a＜1 | B． | a≤1 | C． | a≥1 | D． | a＞1 |
5．下列运算正确的是（ ）
| A． | 2a+3b=5ab | B． | 2（2a-b）=4a-2b | C． | （a2）3=a5 | D． | a6÷a2=a3 |
2．
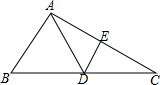如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，△ABC的周长为23，则△ABD的周长为（ ）
如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，△ABC的周长为23，则△ABD的周长为（ ）| A． | 13 | B． | 15 | C． | 17 | D． | 19 |
7．在数$\frac{22}{7}$，0，$\frac{π}{2}$，-1.414中，有理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．已知点M（-3，0），点N是点M关于原点的对称点，点A是函数y=-x+3$\sqrt{2}$图象上的一点，若△AMN是直角三角形，则点A的坐标为（ ）
| A． | （3，3$\sqrt{2}$）或（-3，3+3$\sqrt{2}$） | B． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$）或（$\frac{3}{2}$$\sqrt{2}$，$\frac{3}{2}$$\sqrt{2}$） | ||
| C． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$-3）或（$\sqrt{2}$，2$\sqrt{2}$） | D． | （-3，3+3$\sqrt{2}$）或（3，3$\sqrt{2}$-3）或（$\frac{3}{2}$$\sqrt{2}$，$\frac{3}{2}$$\sqrt{2}$） |