题目内容
19.已知甲地到乙地的路程为320千米,一辆大货车以40千米/小时的速度从甲地前往乙地运送物资,行驶2小时后在途中某地出现故障,大货车司机立即通知技术人员乘小汽车以80千米/小时的速度从甲地按大货车行驶路线赶来维修(通知时间忽略不计),若小汽车到达该地后,经过20分钟修好大货车,然后小汽车立即以原速原路返回甲地,同时大货车也立即加速前往乙地,其速度是原来速度的1.5倍.若大货车到达乙地比小汽车返回甲地晚了m小时,则m=3.分析 由路程=速度×时间可求出大货车出现故障地离甲地的距离,进而可得出大货车出现故障地离乙地的距离,再根据时间=路程÷速度结合大货车到达乙地比小汽车返回甲地晚了m小时,即可得出关于m的一元一次方程,解之即可得出结论.
解答 解:大货车车修好后,小汽车的路程为40×2=80(千米),大货车的路程为320-80=240(千米).
根据题意得:$\frac{240}{40×1.5}$-$\frac{80}{80}$=m,
解得:m=3.
故答案为:3.
点评 本题考查了一元一次方程的应用,根据时间=路程÷速度结合大货车到达乙地比小汽车返回甲地晚了m小时,列出关于m的一元一次方程是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
7.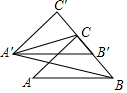 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
 把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
把△ABC沿BC方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )| A. | 增大 | B. | 减小 | C. | 不变 | D. | 不确定 |
4.某新建火车站站前有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),则人行通道的宽度是( )


| A. | 1 米 | B. | 2米 | C. | $\frac{26}{3}$米 | D. | 2米或$\frac{26}{3}$米 |
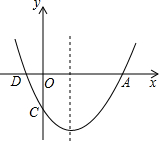 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1.
 如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.