题目内容
12. 如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.
如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.
分析 根据点的坐标性质结合勾股定理得出AD,BD的长,进而得出答案.
解答  解:如图所示:过点A作AC⊥y轴于点C,
解:如图所示:过点A作AC⊥y轴于点C,
∵A(3,4),D(0,1),
∴AC=3,DC=3,
∴AD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵D(0,1),B(1,0),
∴DO=BO=1,
∴BD=$\sqrt{2}$,
∴光线从点A到点B经过的路径长为:3$\sqrt{2}$+$\sqrt{2}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 此题主要考查了勾股定理以及坐标的性质,得出AD,BD的长是解题关键.

练习册系列答案
相关题目
3.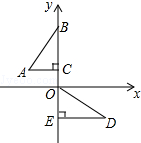 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移2 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移2 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移6 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移6 |
7.函数y=m${x}^{{m}^{2}-3}$+2-m是正比例函数,则m的值为( )
| A. | m不为0 | B. | m=2 | C. | m=-2 | D. | m=2或-2 |
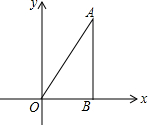 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$). 如图⊙O的半径为3,AB=BC,CD=DE,则阴影部分的面积和为$\frac{9}{4}$π.
如图⊙O的半径为3,AB=BC,CD=DE,则阴影部分的面积和为$\frac{9}{4}$π.