题目内容
4.若xm+1y5和$\frac{2{x}^{4}{y}^{2n+1}}{5}$是同类项,则2m-3mn=-12.分析 根据同类项的定义可先求得m和n的值,从而求出2m-3mn的值.
解答 解:由同类项的定义可知m+1=4,2n+1=5,
解得:m=3,n=2,
则2m-3mn=-12.
故答案为:-12.
点评 此题考查同类项问题,代数式的求值也是中考中常见的试题,要求代数式的值,关键是求出代数式中的字母的值,本题根据同类项即可求解字母的值.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
9.若a4•ax-1=a5,则x等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.若$\frac{m}{2}+1$与$\frac{2m-7}{3}$互为相反数,则m=( )
| A. | 2 | B. | -2 | C. | $\frac{8}{7}$ | D. | -$\frac{8}{7}$ |
14.下面去括号正确的是( )
| A. | 3(a-b)=3a-b | B. | a-(b-c)=a+b-c | C. | a+(b+c)=a+b+c | D. | -(a-2b)=-a-2b |
 如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.
如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.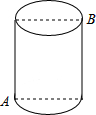 如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是10cm.
如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是10cm.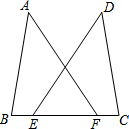 如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.
如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.