题目内容
20.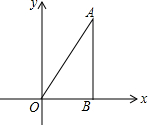 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
分析 先利用一次函数图象上点的坐标特征确定A(2,2$\sqrt{3}$),再分类讨论:当△ABO绕点B顺时针旋转60°得到△CBD,如图1,作CH⊥x轴,则BC=AB=2$\sqrt{3}$,∠ABC=60°,在Rt△BCH中利用含30度的直角三角形三边的关系得到CH=$\frac{1}{2}$BC=$\sqrt{3}$,BH=$\sqrt{3}$CH=3,则OH=OB+BH=5,则此时C点坐标为(5,$\sqrt{3}$);当△ABO绕点B逆时针旋转60°得到△CBD,如图2,作CH⊥x轴,同样方法可计算出CH=$\sqrt{3}$,BH=3,而OH=BH-OB=1,则此时C点坐标为(-1,$\sqrt{3}$).
解答 解:∵点B的坐标为(2,0),
而AB⊥x轴,
∴A的横坐标为2,
当x=2时,y=$\sqrt{3}$x=2$\sqrt{3}$,
∴A(2,2$\sqrt{3}$),
当△ABO绕点B顺时针旋转60°得到△CBD,如图1,作CH⊥x轴,则BC=AB=2$\sqrt{3}$,∠ABC=60°,
在Rt△BCH中,∵∠HBC=30°,
∴CH=$\frac{1}{2}$BC=$\sqrt{3}$,BH=$\sqrt{3}$CH=3,
∴OH=OB+BH=2+3=5,
∴C点坐标为(5,$\sqrt{3}$);
当△ABO绕点B逆时针旋转60°得到△CBD,如图2,作CH⊥x轴,则BC=AB=2$\sqrt{3}$,∠ABC=60°,
在Rt△BCH中,∵∠HBC=30°,
∴CH=$\frac{1}{2}$BC=$\sqrt{3}$,BH=$\sqrt{3}$CH=3,
∴OH=BH-OB=3-2=1,
∴C点坐标为(-1,$\sqrt{3}$),
综上所述,点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
故答案为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°;记住关于原点对称的点的坐标特征.解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.

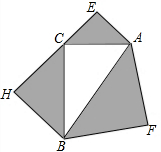 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.
如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.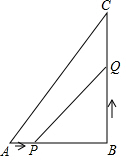 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发. 如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.
如图,一束光线从点A(3,4)出发,经过y轴上点(0,1)反射后经过点B(1,0),则光线从点A到点B经过的路径长为4$\sqrt{2}$.