题目内容
7.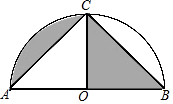 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.
分析 先利用圆周角定理得到∠ACB=90°,则可判断△ACB为等腰直角三角形,接着判断△AOC和△BOC都是等腰直角三角形,于是得到S△AOC=S△BOC,然后根据扇形的面积公式计算图中阴影部分的面积.
解答 解:∵AB为直径,
∴∠ACB=90°,
∵AC=BC=$\sqrt{2}$,
∴△ACB为等腰直角三角形,
∴OC⊥AB,
∴△AOC和△BOC都是等腰直角三角形,
∴S△AOC=S△BOC,OA=$\frac{\sqrt{2}}{2}$AC=1,
∴S阴影部分=S扇形AOC=$\frac{90•π×{1}^{2}}{360}$=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查了扇形面积的计算:圆面积公式:S=πr2,(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.求阴影面积常用的方法:①直接用公式法; ②和差法; ③割补法.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.

练习册系列答案
相关题目
18.在同一平面内,已知线段AB的长为10厘米,点A、B到直线l的距离分别为6厘米和4厘米,则符合条件的直线l的条数为( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
15.一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
12.方程x2-8x+17=0的根的情况是( )
| A. | 两实数根的和为-8 | B. | 两实数根的积为17 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
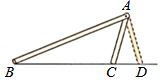 教材中有如下一段文字:
教材中有如下一段文字: 如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长.
如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长.