题目内容
12.方程x2-8x+17=0的根的情况是( )| A. | 两实数根的和为-8 | B. | 两实数根的积为17 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
分析 根据方程的系数结合根的判别式,即可得出△=-4<0,由此可得出方程没有实数根.
解答 解:∵在方程x2-8x+17=0中,△=(-8)2-4×1×17=-4<0,
∴方程x2-8x+17=0没有实数根.
故选D.
点评 本题考查了根的判别式,熟练掌握“当△<0时,方程无实数根”是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
2.已知$\left\{\begin{array}{l}x=3\\ y=5\end{array}\right.$是方程mx-2y=2解,则m的值为( )
| A. | $\frac{8}{5}$ | B. | $\frac{5}{3}$ | C. | 4 | D. | $-\frac{8}{3}$ |
3.函数y=x2+3x+2的图象如图1所示,根据图象回答问题:
(1)当x<-2或x>-1时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题:
①函数y=$\sqrt{(x+1)(x+2)}$的自变量x的取值范围是x≤-2或x≥-1;
②如表是函数y=$\sqrt{(x+1)(x+2)}$的几组y与x的对应值.
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质:关于直线x=-1.5对称.

(1)当x<-2或x>-1时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题:
①函数y=$\sqrt{(x+1)(x+2)}$的自变量x的取值范围是x≤-2或x≥-1;
②如表是函数y=$\sqrt{(x+1)(x+2)}$的几组y与x的对应值.
| x | … | -7 | -6 | -4 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | … |
| y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
③写出该函数的一条性质:关于直线x=-1.5对称.
17.若a+3=0,则a的相反数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
4.一个数和它的倒数相等,那么这个数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
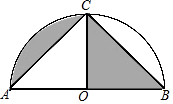 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.