题目内容
15．一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{3}$ |
分析 直接利用概率公式求解．
解答 解：从该盒子中任意摸出一个球，摸到黄球的概率=$\frac{4}{6}$=$\frac{2}{3}$．
故选A．
点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．
练习册系列答案
相关题目
5．在求3x的倒数的值时，嘉淇同学将3x看成了8x，她求得的值比正确答案小5，依上述情形，所列关系式成立的是（ ）
| A． | $\frac{1}{3x}$=$\frac{1}{8x}$+5 | B． | $\frac{1}{3x}$=$\frac{1}{8x}$-5 | C． | $\frac{1}{3x}$=8x-5 | D． | $\frac{1}{3x}$=8x+5 |
3．函数y=x2+3x+2的图象如图1所示，根据图象回答问题：
（1）当x＜-2或x＞-1时，x2+3x+2＞0；
（2）在上述问题的基础上，探究解决新问题：
①函数y=$\sqrt{（x+1）（x+2）}$的自变量x的取值范围是x≤-2或x≥-1；
②如表是函数y=$\sqrt{（x+1）（x+2）}$的几组y与x的对应值．
如图2，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点的大概位置，请你根据描出的点，画出该函数的图象：
③写出该函数的一条性质：关于直线x=-1.5对称．
（1）当x＜-2或x＞-1时，x2+3x+2＞0；
（2）在上述问题的基础上，探究解决新问题：
①函数y=$\sqrt{（x+1）（x+2）}$的自变量x的取值范围是x≤-2或x≥-1；
②如表是函数y=$\sqrt{（x+1）（x+2）}$的几组y与x的对应值．
| x | … | -7 | -6 | -4 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | … |
| y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
③写出该函数的一条性质：关于直线x=-1.5对称．
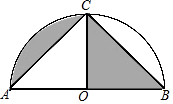如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC=$\sqrt{2}$，则图中阴影部分的面积是$\frac{π}{4}$．
4．一个数和它的倒数相等，那么这个数是（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | ±1 |