题目内容
18.在同一平面内,已知线段AB的长为10厘米,点A、B到直线l的距离分别为6厘米和4厘米,则符合条件的直线l的条数为( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
分析 根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.画出图形进行判断.
解答 解:①如图1 ,
,
在线段AB的两旁可分别画一条满足条件的直线;
②作线段AB的垂线,将线段AB分成6cm,4cm两部分.
故选:B.
点评 本题考查了点到直线的距离,即直线外一点到这条直线的垂线段的长度,注意距离都是非负数.此题还可分别以A、B为圆心、以6cm和4cm为半径作圆,利用直线和两圆的位置关系来进行解答.

练习册系列答案
相关题目
13.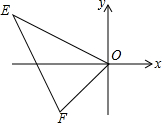 在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2:1,把△EFO缩小,则点E的对应点E′的坐标是( )
在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2:1,把△EFO缩小,则点E的对应点E′的坐标是( )
 在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2:1,把△EFO缩小,则点E的对应点E′的坐标是( )
在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2:1,把△EFO缩小,则点E的对应点E′的坐标是( )| A. | (-2,1) | B. | (-8,4) | C. | (-2,1)或(2,-1) | D. | (-8,4)或(8,-4) |
3.函数y=x2+3x+2的图象如图1所示,根据图象回答问题:
(1)当x<-2或x>-1时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题:
①函数y=$\sqrt{(x+1)(x+2)}$的自变量x的取值范围是x≤-2或x≥-1;
②如表是函数y=$\sqrt{(x+1)(x+2)}$的几组y与x的对应值.
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质:关于直线x=-1.5对称.

(1)当x<-2或x>-1时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题:
①函数y=$\sqrt{(x+1)(x+2)}$的自变量x的取值范围是x≤-2或x≥-1;
②如表是函数y=$\sqrt{(x+1)(x+2)}$的几组y与x的对应值.
| x | … | -7 | -6 | -4 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | … |
| y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
③写出该函数的一条性质:关于直线x=-1.5对称.
8.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{4(a+1)}$ |
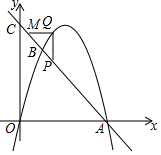 如图,在平面直角坐标系中,点A是抛物线y=-$\frac{1}{2}$x2+4x与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点C.点M、P在线段AC上(不含端点),点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴.设点P横坐标为m.
如图,在平面直角坐标系中,点A是抛物线y=-$\frac{1}{2}$x2+4x与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点C.点M、P在线段AC上(不含端点),点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴.设点P横坐标为m. 在矩形ABCD中,AB=6,BC=8,△ABD绕B点顺时针旋转90°到△BEF,连接DF,则DF=10$\sqrt{2}$.
在矩形ABCD中,AB=6,BC=8,△ABD绕B点顺时针旋转90°到△BEF,连接DF,则DF=10$\sqrt{2}$.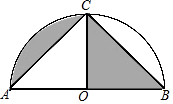 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.