题目内容
16. 如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长.
如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长.
分析 根据锐角三角函数的定义求出AC,根据勾股定理求出AB即可.
解答 解:∵∠C=90°,BC=12,$tanA=\frac{BC}{AC}=\frac{3}{4}$,
∴AC=16,
∵AB2=AC2+BC2,
∴AB2=162+122=400,
∴AB=20.
点评 本题考查了锐角三角函数的定义和勾股定理,能根据锐角三角函数的定义求出AC是解此题的关键.

练习册系列答案
相关题目
4.一个数和它的倒数相等,那么这个数是( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
11.若|a-1|+(b+3)2=0,则b-a-$\frac{1}{2}$的值为( )
| A. | -5$\frac{1}{2}$ | B. | -4$\frac{1}{2}$ | C. | -3$\frac{1}{2}$ | D. | -1$\frac{1}{2}$ |
8.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{48}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{4(a+1)}$ |
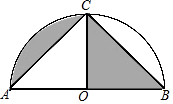 如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=$\sqrt{2}$,则图中阴影部分的面积是$\frac{π}{4}$.