题目内容
17.先化简,再求值:$\frac{m-3}{{3{m^2}-6m}}÷({m+2-\frac{5}{m-2}})$,其中m=-1.分析 先根据分式混合运算的法则把原式进行化简,再把m=-1代入进行计算即可.
解答 解:原式=$\frac{m-3}{3m(m-2)}$÷$\frac{{m}^{2}-9}{m-2}$
=$\frac{m-3}{3m(m-2)}$•$\frac{m-2}{(m+3)(m-3)}$
=$\frac{1}{{3m({m+3})}}$.
当m=-1时,原式=$\frac{1}{3×(-1)(-1+3)}$=$-\frac{1}{6}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
5.某工厂欲将n件产品运往A、B、C三地销售,要求运往C地的件数是运往A地的件数的2倍,各地的运费如表所示.设安排x件产品运往A地.
(1)当n=200时:
①根据信息填表:
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
| 工厂 | A地 | B地 | C地 |
| 运费 | 30元/件 | 8元/件 | 25元/件 |
①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
(2)若总运费为5800元,求n的最小值.
6. 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
 如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )
如图,在△ABC中,AB=AC,EF∥BC,∠A=40°,则∠AEF的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 140° |
7.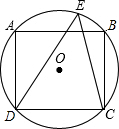 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )| A. | 40° | B. | 45° | C. | 48° | D. | 50° |
 已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.
已知,如图,?ABCD中,CN=AM,AE=CF,求证:EN∥MF.