题目内容
5.某工厂欲将n件产品运往A、B、C三地销售,要求运往C地的件数是运往A地的件数的2倍,各地的运费如表所示.设安排x件产品运往A地.| 工厂 | A地 | B地 | C地 |
| 运费 | 30元/件 | 8元/件 | 25元/件 |
①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
(2)若总运费为5800元,求n的最小值.
分析 (1)①根据运往B地的产品件数=总件数-运往A地的产品件数-运往B地的产品件数;运费=相应件数×一件产品的运费,即可补全图表;
②根据运往B地的件数不多于运往C地的件数,总运费不超过4000元列出不等式组,求出x的取值范围,再根据x只能取整数,即可得出运输方案;
(2)总运费=A产品的运费+B产品的运费+C产品的运费,进而根据函数的增减性及(1)中②得到的x的取值求得n的最小值即可.
解答 解:(1)①根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 200-3x | 2x | 200 |
| 运费(元) | 30x | -24x+1600 | 50x | 56x+1600 |
$\left\{\begin{array}{l}{200-3x≤2x}\\{56x+1600≤4000}\end{array}\right.$,
解得40≤x≤42$\frac{6}{7}$,
∵x为整数,
∴x=40或41或42,
∴有三种方案,
当运往A地40件,B地80件,C地80件;
(2)由题意,得30x+8(n-3x)+50x=5800,
整理,得n=725-7x.
∵n-3x≥0,
∴725-7x-3x≥0,
∴-10x≥-725,
∴x≤72.5,
又∵x≥0,
∴0≤x≤72.5且x为正整数.
∵n随x的增大而减少,
∴当x=72时,n有最小值为221.
点评 考查一次函数的应用;得到总运费的关系式是解决本题的关键;注意结合自变量的取值得到n的最小值.

练习册系列答案
相关题目
 如图,点A为反比例函数y=$\frac{k}{x}$(x>0)图象上的一点,过点A作AD⊥x轴于点D,连接OA,△AOD的面积为$\frac{3}{2}$.
如图,点A为反比例函数y=$\frac{k}{x}$(x>0)图象上的一点,过点A作AD⊥x轴于点D,连接OA,△AOD的面积为$\frac{3}{2}$.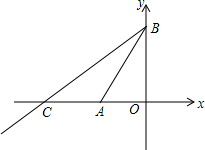 如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C,且∠CBA=45°,求直线BC的解析式.
如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C,且∠CBA=45°,求直线BC的解析式.