题目内容
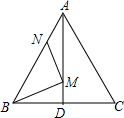 如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是
如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是考点:轴对称-最短路线问题
专题:
分析:过C作CN⊥AB于N,交AD于M,连接BM,根据两点之间线段最短和垂线段最短得出此时BM+MN最小,由于C和B关于AD对称,则BM+MN=CN,根据勾股定理求出CN,即可求出答案.
解答: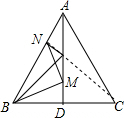 解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
∵等边△ABC中,AD平分∠CAB,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CM=BM,
即BM+MN=CM+MN=CN,
∵CN⊥AB,
∴∠CNB=90°,CN是∠ACB的平分线,AN=BN(三线合一),
∵∠ACB=60°,
∴∠BCN=30°,
∵AB=6,
∴BN=
AB=3,
在△BCN中,由勾股定理得:CN=
=
=3
,即BM+MN的最小值是3
.
故答案为3
.
 解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,∵等边△ABC中,AD平分∠CAB,
∴AD⊥BC,
∴AD是BC的垂直平分线(三线合一),
∴C和B关于直线AD对称,
∴CM=BM,
即BM+MN=CM+MN=CN,
∵CN⊥AB,
∴∠CNB=90°,CN是∠ACB的平分线,AN=BN(三线合一),
∵∠ACB=60°,
∴∠BCN=30°,
∵AB=6,
∴BN=
| 1 |
| 2 |
在△BCN中,由勾股定理得:CN=
| BC2-BN2 |
| 62-32 |
| 3 |
| 3 |
故答案为3
| 3 |
点评:本题考查的是轴对称-最短路线问题,涉及到等边三角形的性质,勾股定理,轴对称的性质,等腰三角形的性质等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程2(x+1)2=5x的根的情况( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、以上答案都不对 |
下列关于邻补角的说法,正确的是( )
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
 如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.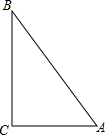 如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米. P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.