题目内容
 P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.考点:旋转的性质,等边三角形的判定与性质,勾股定理的逆定理
专题:
分析:将△BPC绕点B逆时针旋转60°得到△ABD,根据旋转的性质可得BD=PB=4,AD=PC=3,∠BPC=∠ADB,判断出△BDP是等边三角形,根据等边三角形的性质可得PD=PB,∠BDP=60°,利用勾股定理逆定理判断出△ADP是直角三角形,∠ADP=90°,然后求出∠ADB,即可得解.
解答: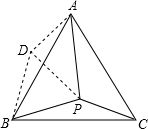 解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,
解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,
由旋转的性质得,BD=PB=4,AD=PC=3,∠BPC=∠ADB,
所以,△BDP是等边三角形,
所以,PD=PB=4,∠BDP=60°,
∵AD2+DP2=32+42=25,PA2=52=25,
∴AD2+DP2=PA2,
∴△ADP是直角三角形,∠ADP=90°,
∴∠ADB=60°+90°=150°,
∴∠BPC=150°.
 解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,
解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,由旋转的性质得,BD=PB=4,AD=PC=3,∠BPC=∠ADB,
所以,△BDP是等边三角形,
所以,PD=PB=4,∠BDP=60°,
∵AD2+DP2=32+42=25,PA2=52=25,
∴AD2+DP2=PA2,
∴△ADP是直角三角形,∠ADP=90°,
∴∠ADB=60°+90°=150°,
∴∠BPC=150°.
点评:本题考查了旋转的性质,勾股定理逆定理,等边三角形的判定与性质,利用旋转作辅助线构造出直角三角形和等边三角形是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则
如图,正方形ABCD的对角线相交于O,点F在AD上,AD=3AF,△AOF的外接圆交AB于E,则| AE |
| AF |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
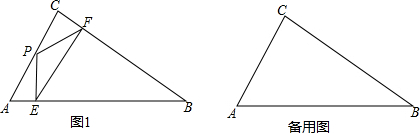
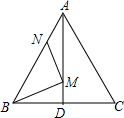 如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是
如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是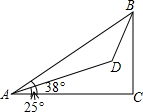 某勘测队在山脚测得山顶的仰角为38°,沿倾斜角为25°的山坡前进800米后,又测得山顶的仰角为62°,求山的高度(精确到0.1米).(cos13°=0.9744,sin13°=0.2250,cot24°=2.246,sin38°=0.6157).
某勘测队在山脚测得山顶的仰角为38°,沿倾斜角为25°的山坡前进800米后,又测得山顶的仰角为62°,求山的高度(精确到0.1米).(cos13°=0.9744,sin13°=0.2250,cot24°=2.246,sin38°=0.6157).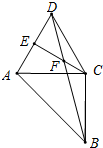 如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.
如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.