题目内容
3.解方程组(1)$\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+y+z=6}\\{x+2y-3z=4}\\{2x-y+z=5}\end{array}\right.$.
分析 (1)根据解二元一次方程组的方法先将二元一次方程组转化为一元一次方程,即可解答本题;
(2)先将三元一次方程组转化为二元一次方程组,再转化为一元一次方程,本题得以解决.
解答 解:(1)$\left\{\begin{array}{l}{x+y=5}&{①}\\{2x-y=1}&{②}\end{array}\right.$
①+②,得
3x=6,
解得,x=2,
将x=2代入①,得y=3,
故原方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+y+z=6}&{①}\\{x+2y-3z=4}&{②}\\{2x-y+z=5}&{③}\end{array}\right.$
①×3+②,得
4x+5y=22④
③-①,得
x-2y=-1⑤
④-⑤×4,得
13y=26,
解得,y=2,
将y=2代入⑤,得x=3,
将x=3,y=2代入①,得z=1,
故原方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=1}\end{array}\right.$.
点评 本题考查解二元一次方程组、解三元一次方程组,解题的关键是明确消元的思想,会解方程组的方法.

练习册系列答案
相关题目
 反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.
反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.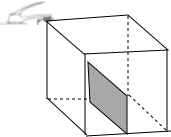 如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )
如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )
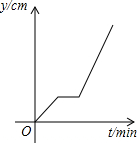
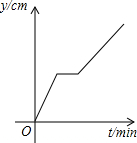
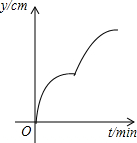
 如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC=40°.
如图,AB与CD相交于点O,∠AOD+∠BOC=280°,则∠AOC=40°. 如图,AB⊥CD于点O,直线EF过点O,若∠AOE=55°,则∠DOF度数为35°.
如图,AB⊥CD于点O,直线EF过点O,若∠AOE=55°,则∠DOF度数为35°.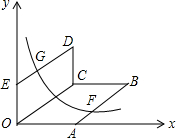 如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9.
如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=58°,则∠3的度数等28°.
如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=58°,则∠3的度数等28°.