题目内容
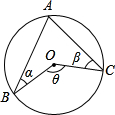 如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )
如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )| A、θ=α+β |
| B、θ+α+β=360° |
| C、θ+α+β=180° |
| D、θ=2α+2β |
考点:圆周角定理
专题:
分析:连接AO并延长,交⊙O于点D,根据圆周角定理可得出∠BOD=2∠BAO,∠COD=2∠CAO,从而得出θ=α+β.
解答:
 解:连接AO并延长,交⊙O于点D,
解:连接AO并延长,交⊙O于点D,
∵OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOD=2∠BAO,∠COD=2∠CAO,
∴∠BOC=2(∠BAO+∠CAO),
∵∠ABO=α,∠ACO=β,∠BOC=θ,
∴θ=2(α+β)=2α+2β,
故选D.
 解:连接AO并延长,交⊙O于点D,
解:连接AO并延长,交⊙O于点D,∵OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BOD=2∠BAO,∠COD=2∠CAO,
∴∠BOC=2(∠BAO+∠CAO),
∵∠ABO=α,∠ACO=β,∠BOC=θ,
∴θ=2(α+β)=2α+2β,
故选D.
点评:本题考查了圆周角定理,以及等腰三角形的性质,掌握同弧所对的圆周角是圆心角的一半是解题的关键.

练习册系列答案
相关题目
在下列实数中,无理数是( )
A、-
| |||
| B、3.14 | |||
C、
| |||
D、
|
△ABC中有六个元素,只要已知其中的某些元素就可以作出这个三角形,根据以下给出的条件,可作出△ABC的有( )个.
①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两角和其中一角的对边.
①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两角和其中一角的对边.
| A、1 | B、2 | C、3 | D、4 |
 如图,线段AB=DE,点C为线段AE的中点,下列式子中不正确的是( )
如图,线段AB=DE,点C为线段AE的中点,下列式子中不正确的是( )| A、BC=CD |
| B、CD=AC-AB |
| C、CD=AD-CE |
| D、CD=DE |
 如图,已知AB∥CD,AE∥CF,BF=DE
如图,已知AB∥CD,AE∥CF,BF=DE
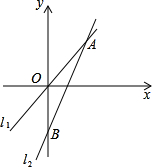 如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.
如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.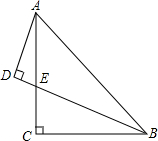 如图,在Rt△ABC中,∠C=90°,AC=BC,BE平分∠ABC交AC于E,点D在BE的延长线上,AD⊥BE.
如图,在Rt△ABC中,∠C=90°,AC=BC,BE平分∠ABC交AC于E,点D在BE的延长线上,AD⊥BE.