题目内容
 等边△ABC中,D在AB上,E在BC延长线上,AD=CE,DE交AC于G.求证:点G是DE中点.
等边△ABC中,D在AB上,E在BC延长线上,AD=CE,DE交AC于G.求证:点G是DE中点.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:过点D作DF∥BC交AC于F,根据两直线平行,内错角相等可得∠FDG=∠E,判断出△ADF是等边三角形,根据等边三角形的性质可得AD=DF,再求出DF=CE,然后利用“角角边”证明△DFG和△ECG全等,根据全等三角形对应边相等可得DG=EG,再根据线段中点的定义证明即可.
解答:
 证明:如图,过点D作DF∥BC交AC于F,
证明:如图,过点D作DF∥BC交AC于F,
则∠FDG=∠E,
∵△ABC的等边三角形,
∴∠A=∠B=∠ACB=60°,
∵DF∥BC,
∴∠ADF=∠AFD=60°,
∴△ADF是等边三角形,
∴AD=DF,
∵AD=CE,
∴DF=CE,
在△DFG和△ECG中,
,
∴△DFG≌△ECG(AAS),
∴DG=EG,
∴点G是DE中点.
 证明:如图,过点D作DF∥BC交AC于F,
证明:如图,过点D作DF∥BC交AC于F,则∠FDG=∠E,
∵△ABC的等边三角形,
∴∠A=∠B=∠ACB=60°,
∵DF∥BC,
∴∠ADF=∠AFD=60°,
∴△ADF是等边三角形,
∴AD=DF,
∵AD=CE,
∴DF=CE,
在△DFG和△ECG中,
|
∴△DFG≌△ECG(AAS),
∴DG=EG,
∴点G是DE中点.
点评:本题考查了全等三角形的判定与性质,等边三角形的判定与性质,作辅助线构造出全等三角形和等边三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 如图,不能推出a∥b的条件是( )
如图,不能推出a∥b的条件是( )| A、∠1=∠3 |
| B、∠1=∠4 |
| C、∠2=∠4 |
| D、∠2+∠3=180° |
在下列实数中,无理数是( )
A、-
| |||
| B、3.14 | |||
C、
| |||
D、
|
某种生物细胞的直径是0.000000012cm,用科学记数法表示这个数,正确的是( )
| A、12×10-7cm |
| B、1.2×10-7cm |
| C、12×10-8cm |
| D、1.2×10-8cm |
 如图,已知E、A、B三点在同一直线上,AD是∠EAC的平分线,AD∥BC,∠B=50°,求∠EAD,∠C,∠BAC的度数.
如图,已知E、A、B三点在同一直线上,AD是∠EAC的平分线,AD∥BC,∠B=50°,求∠EAD,∠C,∠BAC的度数.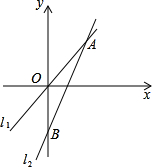 如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.
如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.