题目内容
4．某商品的进价为每件40元，售价为每件50元，每个月可卖出210件，如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元），设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元．（1）求y与x的函数关系式；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
（3）请你直接写出售价在什么范围时，每个月的利润不低于2200元？
分析 （1）根据进价为每件40元，售价为每件50元，每个月可卖出210件，再根据每件商品的售价每上涨1元，则每个月少卖10件和销售利润=件数×每件的利润列出关系式，即可得出答案．
（2）根据（1）得出的函数关系式，再进行配方得出y=-10（x-5.5）2+2402.5，当x=5.5时y有最大值，从而得出答案；
（3）由“每个月的利润不低于2200元”列出关于x的不等式，解之可得．
解答 解：（1）由题意得：y=（210-10x）（50+x-40）
=-10x2+110x+2100（0＜x≤15且x为整数）；
（2）根据（1）得：y=-10x2+110x+2100=-10（x-5.5）2+2402.5，
∵a=-10＜0，
∴当x=5.5时，y有最大值2402.5．
∵0＜x≤15，且x为整数，
当x=5时，50+x=55，y=2400（元），
当x=6时，50+x=56，y=2400（元）
∴当售价定为每件55或56元，每个月的利润最大，最大的月利润是2400元；
（3）根据题意得，-10x2+110x+2100≥2200，
解得：1≤x≤10，
故1≤x≤10且x为整数时，每个月的利润不低于2200元．
点评 本题考查二次函数的实际应用，关键是读懂题意，找出之间的等量关系，根据每天的利润=一件的利润×销售件数，建立函数关系式，此题为数学建模题，借助二次函数解决实际问题．
练习册系列答案
相关题目
14．某检修小组从A地出发，在东西向的铁路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中六次行驶情况记录如下（单位：公里）
（1）求这天结束时距A地多远？
（2）若每公里耗油1.2升，问共耗油多少升？
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| -5 | +7 | -9 | +10 | +6 | -5 |
（2）若每公里耗油1.2升，问共耗油多少升？
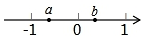有理数a，b在数轴上对应的位置如图所示，那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2．
如图，矩形ABOC的顶点A在反比例函数y=-$\frac{4}{x}$（x＜0）的图象上，则矩形ABOC的面积等于（ ）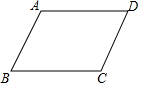
如图，如果∠B=65°，AD∥BC，AB∥DC，那么∠A=115°；∠D=65°；∠B=∠D．
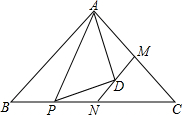如图，等腰直角三角形ABC，斜边上一动点P，连接AP，以AP为斜边作等腰直角三角形，顶点为D，点M是AC边中点，连接MD，延长交斜边于点N，求证：BN=CN．