题目内容
17.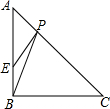 如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.
如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.
分析 由B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
解答 解::如图:作等腰直角三角形ABC关于AC的对称直角三角形ADC,
连接DE,与AC交于点P,根据两点之间,线段最短得到ED就是PB+PE的最小值,
∵等腰直角三角形ABC中,∠BAC=45°,
∴∠DAC=45°,
∴∠DAE=90°,
∵B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵AB=CB=4,BE=1,
∴AE=3,AD=CB=4,
由勾股定理得,DE=5.
故答案为:5.
点评 本题考查了直角三角形的性质,勾股定理,轴对称-最短路线问题等知识点的理解和掌握,能求出PE+PB=DE的长是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某商场计划购进甲,乙两种空气净化机共500台,这两种空气净化机的进价、售价如下表:
解答下列问题:
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?
| 进价(元/台) | 售价(元/台) | |
| 甲种空气净化机 | 3000 | 3500 |
| 乙种空气净化机 | 8500 | 10000 |
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?
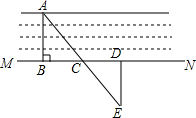 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
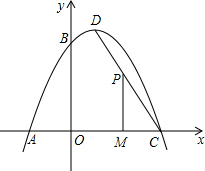 如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.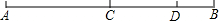 如图,点C,D在线段AB上,CD=4cm,AB=12cm,则图中所有线段的和是多少?
如图,点C,D在线段AB上,CD=4cm,AB=12cm,则图中所有线段的和是多少?