题目内容
9.(1)计算:(-1)2-$\sqrt{16}+{(-2)^0}$;(2)已知:-8(x-3)3=27,求x的值;
(3)计算:$\frac{3}{2}\sqrt{12}+6\sqrt{\frac{3}{4}}-3\sqrt{\frac{1}{3}}$.
分析 (1)先根据数的乘方及开方法则、0指数幂的运算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先把方程两边同时除以-8,利用直接开方法求出x的值即可;
(3)根据先把各根式化为最减二次根式的形式,再合并同类项即可.
解答 解:(1)(-1)2-$\sqrt{16}+{(-2)^0}$
=1-4+1
=-2;
(2)-8(x-3)3=27,
方程两边同时除以-8得,(x-3)3=-$\frac{27}{8}$,
${(x-3)^3}=-\frac{27}{8}$.
.$x-3=-\frac{3}{2}$.
$x=\frac{3}{2}$.
(3)$\frac{3}{2}\sqrt{12}+6\sqrt{\frac{3}{4}}-3\sqrt{\frac{1}{3}}$
=$3\sqrt{3}$+$3\sqrt{3}$-$\sqrt{3}$
=5$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
19. 如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )
如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )
 如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )
如图,菱形ABCD中,对角线AC、BD交于点O,若AC=4,BD=2,则∠1的余弦值为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
20. 如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
 如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 5 |
4.二次函数y=(x-5)2+7的最小值是( )
| A. | -7 | B. | 7 | C. | -5 | D. | 5 |
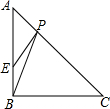 如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.
如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.