题目内容
5.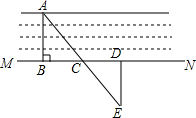 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
分析 根据题意可得∠ABC=∠EDC=90°,再加上条件BC=CD,对顶角∠ACB=∠DCE,可利用ASA定理判定△ABC≌△EDC,再根据全等三角形对应边相等可得DE=AB.
解答 解:∵AB⊥MN,DE⊥MN,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,
$\left\{\begin{array}{l}{∠ABC=∠EDC}\\{BC=DC}\\{∠ACB=∠ECD}\end{array}\right.$,
∴△ABC≌△EDC(ASA),
∴DE=AB.
故答案为:ASA,全等三角形对应边相等.
点评 此题主要考查了全等三角形的应用,关键是掌握全等三角形的判定和性质定理.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20. 如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
 如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )
如图,在△ABC中,BD平分∠ABC,与AC交于点D,DE⊥AB于点E,若BC=5,△BCD的面积为5,则ED的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 5 |
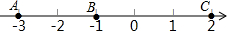 如图,数轴上的点A、B、C分别表示数-3、-1、2.
如图,数轴上的点A、B、C分别表示数-3、-1、2.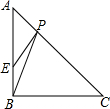 如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.
如图,△ABC中,∠ABC=90°,AB=CB=4,BE=1,P是AC上一动点.则PB+PE的最小值是5.