题目内容
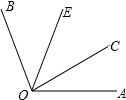 如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB=
如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB=考点:角平分线的定义
专题:
分析:由OE为角平分线,得到∠BOC=2∠COE,由∠COE的度数求出∠COB的度数,再由∠AOC+∠BOC即可求出∠AOB的度数.
解答:解:∵OE是∠COB的平分线,
∴∠COB=2∠COE,
∵∠COE=43°,
∴∠COB=86°,
∵∠AOC=32°,
∴∠AOB=∠AOC+∠COB=118°.
故答案为118°.
∴∠COB=2∠COE,
∵∠COE=43°,
∴∠COB=86°,
∵∠AOC=32°,
∴∠AOB=∠AOC+∠COB=118°.
故答案为118°.
点评:此题考查了角的计算,以及角平分线定义,弄清题意是解本题的关键.

练习册系列答案
相关题目
若抛物线y=x2-4x+3-t(t为实数)在0<x<3
的范围内与x轴有公共点,则t的取值范围为( )
| 1 |
| 2 |
| A、-1<t<3 | ||
| B、-1≤t<3 | ||
C、
| ||
| D、t≥-1 |
 已知∠3=45°,∠1与∠2是对顶角,∠1+∠2=90°,试说明AB∥CD.
已知∠3=45°,∠1与∠2是对顶角,∠1+∠2=90°,试说明AB∥CD.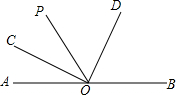 如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD=
如图,OC、OD分别是∠AOP和∠POB的角平分线,那么∠COD= 如图,AB∥CD,AB=CD,点E、F在BC上,BE=CF,试说明此图是中心对称图形的理由.
如图,AB∥CD,AB=CD,点E、F在BC上,BE=CF,试说明此图是中心对称图形的理由.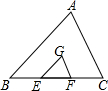 如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC=
如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC= 已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.
已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.