题目内容
18.根据下列条件,确定一次函数的解析式.(1)图象平行于直线y=2x-1,且过点(1,3);
(2)图象经过点(2,-1)且与直线y=-$\frac{1}{2}$x+3相交于y轴上的同一点;
(3)直线y=2x+b与两坐标轴围成的三角形的面积是4.
分析 (1)根据平行直线的解析式的k值相等求出k=2,然后把经过的点代入求出b的值,即可得解.
(2)求得直线与y轴的交点坐标,然后根据待定系数法即可求得;
(3)分别求出一次函数y=2x+b与坐标轴的交点,再根据三角形的面积公式求解即可.
解答 解:(1)∵直线y=kx+b与直线y=2x-1平行,
∴k=2,
∵直线过点(1,3),
∴2×1+b=3,
解得b=1.
故一次函数的解析式为y=2x+1.
(2)由直线y=-$\frac{1}{2}$x+3可知与y轴的解得坐标为(0,3),
∵直线y=kx+b经过(2,-1),(0,3)两点,
∴$\left\{\begin{array}{l}{2k+b=-1}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴一次函数的解析式为y=-2x+3;
(3)∵令x=0,则y=b;令y=0,则x=-$\frac{b}{2}$,
∴一次函数y=2x+b与坐标轴的交点分别为(0,b),(-$\frac{b}{2}$,0).
∵一次函数y=2x+b与坐标轴围成的三角形面积是4,
∴$\frac{1}{2}$|b|•|-$\frac{b}{2}$|=4,解得b=±4.
∴一次函数的解析式为y=2x+4或y=2x-4.
点评 本题考查了待定系数法求直线解析式,两直线平行和相交的问题,两平行直线的解析式的k值相等以及两直线相交的交点坐标一定适合两函数的解析式是解答此题的关键.

练习册系列答案
相关题目
7.如果a>b,那么下列结论一定正确的是( )
| A. | a-3<b-3 | B. | -4a>-4b | C. | 3-a>3-b | D. | $-\frac{a}{3}<-\frac{b}{3}$ |
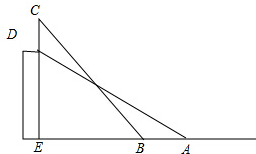 如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).
如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).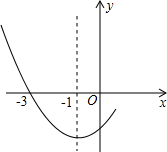 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )