题目内容

19．已知函数y=$\frac{m+2}{x}$的图象在第二、四象限，那么方程mx2-3x+2=0根的情况为（　　）
A．有两个不相等的实数根B．有两个相等的实数根
C．只有一个实数根D．没有实数根

分析 根据反比例函数的性质可得出关于m的一元一次不等式，解不等式可得出m的取值范围，再根据根的判别式△=9-8m即可得出△的取值范围，由此即可得出结论．

解答 解：∵函数y=$\frac{m+2}{x}$的图象在第二、四象限，
∴m+2＜0，
解得：m＜-2．
在方程mx2-3x+2=0中，△=（-3）2-4m×2=9-8m，
∵m＜-2，
∴△=9-8m＞25＞0，
∴方程mx2-3x+2=0有两个不相等的实数根．
故选A．

点评 本题考查了根的判别式意义反比例函数的性质，解题的关键是找出△=9-8m＞25．本题属于基础题，难度不大，解决该题型题目时，根据根的判别式的正负得出方程根的个数是关键．

练习册系列答案
相关题目
9．阅读材料：
解分式不等式$\frac{x+2}{2x-6}＞0$．
解：根据实数的除法法则，同号两数相除得正数，异号两数相除得负数，因此，原不等式可转化为：
①$\left\{\begin{array}{l}{x+2＞0}\\{2x-6＞0}\end{array}\right.$，②$\left\{\begin{array}{l}{x+2＜0}\\{2x-6＜0}\end{array}\right.$．
解不等式组①，得：x＞3．
解不等式组②，得：x＜-2．
所以原分式不等式的解集是x＞3或x＜-2．
请仿照上述方法解分式不等式：$\frac{2x-1}{3x+3}$＜0．
10．（1）计算：（2-π）0-$\sqrt{8}$×$\sqrt{2}$+（$\frac{1}{3}$）-1
（2）如图，过正五边形ABCDE的顶点A作直线l∥BE，求∠1的度数．
7．比较大小：$\frac{1}{2}$＞$\sqrt{2}$-1，-$\sqrt{5}$＜-$\frac{\sqrt{2}}{2}$．
14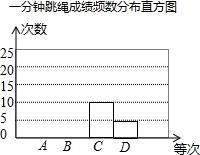．为备战体育中考，李明同学就自己平时1分钟跳绳的训练成绩，做了认真统计，并将训练成绩绘出了如下的频数分布表和频数分布直方图（不完整）．（规定：1分钟跳绳120个以下成绩为D等；120-140个为C等；140-160个为B等；160个以上为A等）
根据以上信息，解答下列问题：
（1）李明同学一共记录了50次平时测试的成绩；
（2）补全频数分布表和频数分布直方图；
（3）李明同学从篮球运球、足球运球、掷实心球、坐位体前屈、1分钟跳绳、立定跳远等六个项目中任选两项作为自己的考试项目，求恰好含有1分钟跳绳项目的概率．
   一分钟跳绳成绩分布表
成绩等次频数（人）频率
D50.1
C100.2
B250.5
A100.2
合计501.00
4．方程4xm-n-5ym+n=6是二元一次方程，则$\sqrt{4m+n}$=2．
11．上网流量、语音通话是手机通信消费的两大主体，目前，某通信公司推出消费优惠新招--“定制套餐”，消费者可根据实际情况自由定制每月上网流量与语音通话时间，并按照二者的阶梯资费标准缴纳通信费．下表是流量与语音的阶梯定价标准．
 流量阶梯定价标准
 使用范围阶梯单价（元/MB） 
 1-100MB a
 101-500MB 0.07
 501MB-20GB b
 语音阶梯定价标准
 使用范围 阶梯资费（元/分钟）
 1-500分钟 0.15
 501-1000分钟 0.12
 1001-2000分钟 m
【小提示：阶梯定价收费计算方法，如600分钟语音通话费=0.15×500+0.12×（600-500）=87元】
（1）甲定制了600MB的月流量，花费48元；乙定制了2GB的月流量，花费120.4元，求a，b的值．（注：1GB=1024MB）
（2）甲的套餐费用为199元，其中含600MB的月流量；丙的套餐费用为244.2元，其中包含1GB的月流量，二人均定制了超过1000分钟的每月通话时间，并且丙的语音通话时间比甲多300分钟，求m的值．
8．如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上，从左向右第3个正方形中的一个顶点A的坐标为（27，9）阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn，则第4个正方形的边长是$\frac{27}{2}$Sn的值为$\frac{{3}^{4n-4}}{{2}^{4n-7}}$
9．下列运算正确的是（　　）
A．4a-a=3B．a6÷a3=a3C．（ab）2=ab2D．（a-b）2=a2-b2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网