题目内容
8. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是$\frac{27}{2}$Sn的值为$\frac{{3}^{4n-4}}{{2}^{4n-7}}$
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是$\frac{27}{2}$Sn的值为$\frac{{3}^{4n-4}}{{2}^{4n-7}}$分析 先根据阴影部分的面积等于一个等腰直角三角形的面积加上梯形的面积再减去一个直角三角形的面积列式求解并根据结果的规律是阴影部分的面积是前一个正方形面积的一半.再根据直线解析式判断出直线与x轴的夹角的正切值为$\frac{1}{2}$,从而得到直线与正方形的边围成的三角形是直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律表示出第2n个正方形的边长,
解答 解:如图,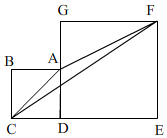 设正方形ABCD的边长为a,正方形DEFG的边长为B,
设正方形ABCD的边长为a,正方形DEFG的边长为B,
∴S△ACF=S△ACD+S梯形ADEF-S△CEF
=$\frac{1}{2}$a2+$\frac{1}{2}$(a+b)×b-$\frac{1}{2}$(a+b)×b=$\frac{1}{2}$a2
∵正比例函数y=$\frac{1}{2}$x的图象与x轴交角的正切值为$\frac{1}{2}$,已知A的坐标为(27,9),
∴∴第3个正方形的边长是9=9×($\frac{3}{2}$)0
∴第4个正方形的边长是$\frac{27}{2}$=9×$\frac{3}{2}$
同理可得第五个正方形的边长为$\frac{81}{4}$=9×($\frac{3}{2}$)2
第六个正方形的边长$\frac{243}{8}$=9×($\frac{3}{2}$)3
…
第2n-1个正方形的边长9×($\frac{3}{2}$)2n-4
第2n个正方形的边长9×($\frac{3}{2}$)2n-3
根据前面得到的规律,Sn=$\frac{1}{2}$×[9×($\frac{3}{2}$)2n-4]2=$\frac{{3}^{4n-4}}{{2}^{4n-7}}$
故答案为$\frac{27}{2}$,$\frac{{3}^{4n-4}}{{2}^{4n-7}}$.
点评 此题是一次函数图象上的点的坐标特征,主要考查了一次函数的性质,正方形的性质,三角形面积的计算,解本题的关键是确定阴影部分面积等于前一个正方形的面积一半.

| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
| A. | 代入法 | |
| B. | 加减法 | |
| C. | 消元,化二元为一元 | |
| D. | 由一个未知数的值求另一个未知数的值 |
| A. | 562.5元 | B. | 875元 | C. | 550元 | D. | 750元 |
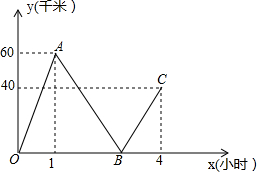 甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题:
甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题: