题目内容
7.比较大小:$\frac{1}{2}$>$\sqrt{2}$-1,-$\sqrt{5}$<-$\frac{\sqrt{2}}{2}$.分析 根据实数大小比较法则比较即可.
解答 解:$\frac{\frac{1}{2}}{\sqrt{2}-1}$=$\frac{1}{2}$($\sqrt{2}$+1),
∴$\frac{1}{2}$>$\sqrt{2}$-1;
$\sqrt{5}$>$\frac{\sqrt{2}}{2}$,
∴-$\sqrt{5}$<-$\frac{\sqrt{2}}{2}$.
点评 本题考查的是实数的大小比较,任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
2.若$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{kx-my=1}\\{mx+ky=8}\end{array}\right.$的解,则k,m的值为( )
| A. | $\left\{\begin{array}{l}{k=2}\\{m=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{k=2}\\{m=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{k=3}\\{m=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{k=-3}\\{m=-2}\end{array}\right.$ |
19.已知函数y=$\frac{m+2}{x}$的图象在第二、四象限,那么方程mx2-3x+2=0根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
17.解二元一次方程组的基本思想是( )
| A. | 代入法 | |
| B. | 加减法 | |
| C. | 消元,化二元为一元 | |
| D. | 由一个未知数的值求另一个未知数的值 |
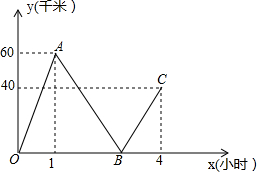 甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题:
甲、乙两车先后从M地驶向N地,甲车出发一小时后,乙车出发,用了两个小时追上甲车,乙车此时马上改变速度又用了1小时到达N地.图中折线表示两车距离y(千米)与甲车行驶时间x(小时)之间的函数关系(0≤x≤4).甲、乙两车匀速行驶.请根据图象信息解答下列问题: