题目内容
10. (1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
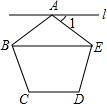
(1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1(2)如图,过正五边形ABCDE的顶点A作直线l∥BE,求∠1的度数.
分析 (1)根据零指数幂的定义、二次根式的乘法法则、负整数指数幂的定义计算,即可得出结果;
(2)首先根据多边形内角和计算公式计算出每一个内角的度数,再根据等腰三角形的性质计算出∠AEB,然后根据平行线的性质可得答案.
解答 (1)解:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
=1-$\sqrt{16}$+3
=1-4+3
=0
(2)解:∵ABCDE是正五边形,
∴∠BAE=(5-2)×180°÷5=108°,AB=AE,
∴∠AEB=∠ABE=(180°-108°)÷2=36°,
∵l∥BE,
∴∠1=∠AEB=36°.
点评 此题考查了零指数幂的定义、二次根式的乘法法则、负整数指数幂的定义、正多边形的内角和定理,以及三角形内角和定理,平行线的性质;熟记有关定义和性质是解决问题的关键.

练习册系列答案
相关题目
20.一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
2.若$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{kx-my=1}\\{mx+ky=8}\end{array}\right.$的解,则k,m的值为( )
| A. | $\left\{\begin{array}{l}{k=2}\\{m=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{k=2}\\{m=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{k=3}\\{m=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{k=-3}\\{m=-2}\end{array}\right.$ |
19.已知函数y=$\frac{m+2}{x}$的图象在第二、四象限,那么方程mx2-3x+2=0根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |