题目内容
9.如图是由边长为2的三个菱形组成的伸缩衣架,每个菱形的内角变化范围是60°到120°,则伸缩衣架的长度l的变化范围是( )
| A. | 2≤l≤2$\sqrt{3}$ | B. | 3≤l≤3$\sqrt{3}$ | C. | 3$\sqrt{3}$≤l≤6$\sqrt{3}$ | D. | 6$≤l≤6\sqrt{3}$ |
分析 首先分别画出菱形的内角是60°与120°的图形,则可得到含30°的直角三角形与等边三角形,继而求得AD=$\sqrt{3}$与1,则可求得伸缩衣架的长度l的变化范围.
解答 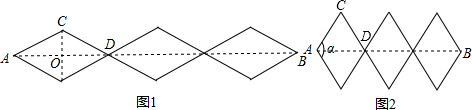 解:如图1,若菱形的内角为60°,
解:如图1,若菱形的内角为60°,
则∠CAD=30°,
∵OC⊥AD,
∴OA=AC•cos30°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴AD=2OA=$\sqrt{3}$,
∴AB=3AD=3$\sqrt{3}$;
如图2,若菱形的内角为120°,
则∠C=180°-120°=60°,
∴△ACD是等边三角形,
∴AD=AC,
∴AB=3AC=3×1=3;
∴伸缩衣架的长度l的变化范围是:3≤l≤3$\sqrt{3}$.
故选B.
点评 此题考查了菱形的性质、含30°角的直角三角形的性质以及等边三角形的判定与性质.注意分别求得菱形的内角是60°与120°时,长度l的值是关键.

练习册系列答案
相关题目
19.已知$\left\{\begin{array}{l}a=2t+3\\ b=3t-1\end{array}\right.$,则用含a的代数式表示b,得( )
| A. | $b=\frac{3a-11}{2}$ | B. | b=3a-1 | C. | $b=\frac{3a-7}{3}$ | D. | $b=\frac{3a+1}{2}$ |
4.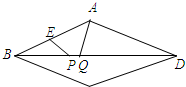 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )| A. | 16 | B. | 21 | C. | 7+$\sqrt{85}$ | D. | 7+$\sqrt{61}$ |
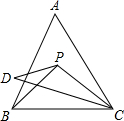 如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.
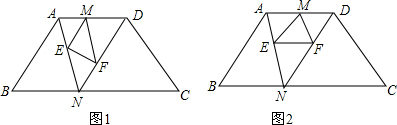
如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.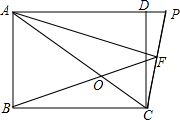 已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.
已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.