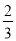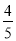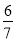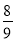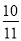题目内容
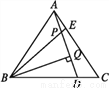
如图,点D,E是正三角形ABC的边BC,AC上的点,且CD=AE,AD,BE相交于点P,BQ⊥AD于点Q,已知BE=7,则AD等于( )
A. 5 B. 6 C. 7 D. 8
 C
【解析】【解析】
∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°.
又∵AE=CD,∴△ABE≌△CAD(SAS),∴AD=BE=7.
故选C.
C
【解析】【解析】
∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°.
又∵AE=CD,∴△ABE≌△CAD(SAS),∴AD=BE=7.
故选C.
探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
 (1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,.
(1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,. 用计算器求tan35°的值,按键顺序是 .
 MODE,tan,35,=.
【解析】
试题分析:本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
试题解析:根据已知一个角的正弦值求这个角的算法:先按MODE,选择模式;再键tan,35,最后按=;得到这个角的函数值.
MODE,tan,35,=.
【解析】
试题分析:本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
试题解析:根据已知一个角的正弦值求这个角的算法:先按MODE,选择模式;再键tan,35,最后按=;得到这个角的函数值. 一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为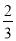 ,应添加几个红球?
,应添加几个红球?
 (1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率...
(1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率... 宁宁同学设计了一个计算程序如下表:
输入数据 | 1 | 2 | 3 | 4 | 5 | … |
输出数据 |
|
|
|
|
| … |
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为_____.
 y=
【解析】【解析】
根据题意,得: .故答案为: .
y=
【解析】【解析】
根据题意,得: .故答案为: . 一个不透明的袋中共有20个球,它们除颜色不同外,其余均相同,其中8个白球,5个黄球,5个绿球,2个红球,则任意摸出一个球是红球的概率是( )
A.  B.
B. 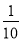 C.
C. 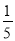 D.
D. 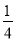
 B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B.
B
【解析】【解析】
∵20个球中红球有2个,∴任意摸出一个球是红球的概率是=,故选B. 将下列不等式的解集分别表示在数轴上:
(1)x≤2;
(2)x>-2.
 (1)见解析;(2)见解析
【解析】分析:根据不等式的解集在数轴上表示出来的方法画数轴即可,根据数轴的性质,实心圆点包括该点用“≥”,“≤”表示,空心圆圈不包括改点用“<”,“>”’表示,大于向右小于向左.
本题解析:
(1)
(2)
(1)见解析;(2)见解析
【解析】分析:根据不等式的解集在数轴上表示出来的方法画数轴即可,根据数轴的性质,实心圆点包括该点用“≥”,“≤”表示,空心圆圈不包括改点用“<”,“>”’表示,大于向右小于向左.
本题解析:
(1)
(2) 若ax>b,ac2<0,则x________.
 <
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<.
<
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<. 在“线段、锐角、三角形、等边三角形”这四个图形中,其中是轴对称图形的有___个,其中对称轴最多的是__________.
 3 等边三角形
【解析】线段有两条对称轴,锐角有一条对称轴,等边三角形有三条对称轴,
故答案为:3,等边三角形.
3 等边三角形
【解析】线段有两条对称轴,锐角有一条对称轴,等边三角形有三条对称轴,
故答案为:3,等边三角形.