题目内容
17．若抛物线y=ax2+bx+c（a＜0）的对称轴为直线x=5，与x轴一交点为A（3，0），则不等式ax2+bx+c＞0的解集是3＜x＜7．分析 根据题意首先得出抛物线与x轴的交点坐标，进而画出大致图象得出不等式的解集．
解答 
解：如图所示：
∵抛物线y=ax2+bx+c（a＜0）的对称轴为直线x=5，与x轴一交点为A（3，0），
∴抛物线与x轴的另一个交点为：（7，0），
∴不等式ax2+bx+c＞0的解集是：3＜x＜7．
故答案为：3＜x＜7．
点评 此题主要考查了二次函数与不等式的解，正确画出二次函数图象是解题关键．
练习册系列答案
相关题目
7．为了奖励本次竞赛获奖同学，刘老师用280元买了A、B两种纪念品，A种纪念品每个20元，B种纪念品每个60元，且A种纪念品比B种纪念品多买了2个，设买了A种纪念品x个，B种纪念品y个，你认为下列哪一个方程组适合求两种纪念品各买了多少个？（ ）
| A． | $\left\{\begin{array}{l}{20x+60y=280}\\{x-y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{60x+20y=280}\\{x-y=2}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{20x+60y=280}\\{y-x=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{60x+20y=280}\\{y-x=2}\end{array}\right.$ |
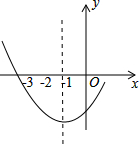如图是二次函数y=ax2+bx-1图象的一部分，其对称轴为x=-1，且过点（-3，0），则（a+b+1）（2-a-b）=2．
如图，EB为半圆O的直径，点A在EB的延长线上，AD切半圆O于点D，BC⊥AD于点C，AB=2，半圆O的半径为2，则BC的长为1．