题目内容
9．用正方形地砖与正六边形地砖不能（填“能”或“不能”）密铺地板．分析 根据密铺的条件，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行密铺，反之则不能．
解答 解：设用x块正方形地砖与y块正六边形地砖能密铺地板，根据题意得
90x+120y=360，
整理得，x=4-$\frac{4}{3}$y，
∵x、y都是正整数，
∴不能密铺．
故答案为：不能．
点评 本题考查了平面镶嵌（密铺），注意两种正多边形的镶嵌应符合多个内角度数和等于360°．
练习册系列答案
相关题目
19．如图1，四边形ABCD是菱形，对角线AC，BD相交于点O，AB=2厘米，∠BAD=60°．P，Q两点同时从点O出发，以1厘米/秒的速度在菱形的对角线及边上运动．设运动的时间为x秒，P，Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，则P，Q的运动路线可能为（ ）
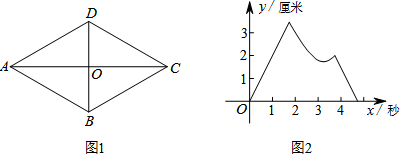
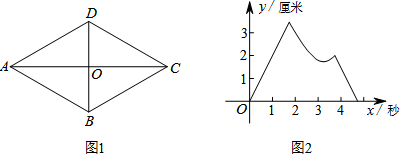
| A． | 点P：O-A-D-C，点Q：O-C-D-O | B． | 点P：O-A-D-O，点Q：O-C-B-O | ||
| C． | 点P：O-A-B-C，点Q：O-C-D-O | D． | 点P：O-A-D-O，点Q：O-C-D-O |
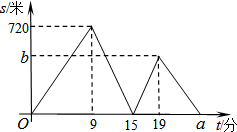小强、小林从学校出发，沿着笔直的道路去少年宫参加书法比赛，小强步行去少年宫一段时间后，小林骑自行车去少年宫，两人均匀速前行．他们两人之间的距离s（米）与小强出发时间t（分）之间的函数关系如图．