题目内容
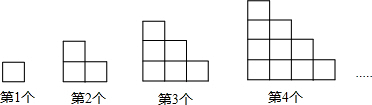
6. 如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为1.
如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为1.
分析 连接OD,根据切线的性质得出OD⊥AD,求出OD∥BC,根据相似三角形的判定得出△BCA∽△ODA,得出比例式,代入求出即可.
解答 解:连接OD,
∵AD切半圆O于点D,
∴OD⊥AD,
∵BC⊥AD,
∴OD∥BC,
∴△BCA∽△ODA,
∴$\frac{OA}{AB}$=$\frac{OD}{BC}$,
∴$\frac{2+2}{2}$=$\frac{2}{BC}$,
∴BC=1,
故答案为:1.
点评 本题考查了切线的性质,相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
16.某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是( )
| A. | 100(1+x) | B. | 100(1+x)2 | C. | 100(1+x2) | D. | 100(1+2x) |
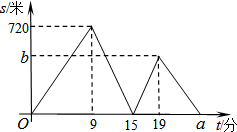 小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.
小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.