题目内容
5.(1)计算:-14+(π-2)0-(tan60°)2+2-1;(2)先化简,再求值:$(x-1-\frac{3}{x+1})÷\frac{{x}^{2}+4x+4}{x+1}$,其中$x=\sqrt{2}-2$.
分析 (1)先根据数的乘方法则、0指数及负整数指数幂的运算法则、特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:(1)原式=-1+1-($\sqrt{3}$)2+$\frac{1}{2}$
=-3+$\frac{1}{2}$
=-$\frac{5}{2}$;
(2)原式=$\frac{{x}^{2}-4}{x+1}$•$\frac{x+1}{(x+2)^{2}}$
=$\frac{(x+2)(x-2)}{x+1}$•$\frac{x+1}{{(x+2)}^{2}}$
=$\frac{x-2}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{\sqrt{2}-2-2}{\sqrt{2}-2+2}$=$\frac{\sqrt{2}-4}{\sqrt{2}}$=$\frac{2-4\sqrt{2}}{2}$=1-2$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
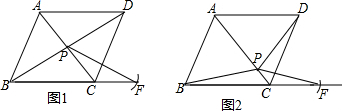
 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A(△EFA与⊙O除切点外无重叠部分),延长FA交CD边于点G,则AG的长是$\frac{\sqrt{865}}{3}$.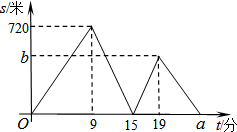 小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.
小强、小林从学校出发,沿着笔直的道路去少年宫参加书法比赛,小强步行去少年宫一段时间后,小林骑自行车去少年宫,两人均匀速前行.他们两人之间的距离s(米)与小强出发时间t(分)之间的函数关系如图.