��Ŀ����
��ͼ��������ABCD�ı߳�Ϊ4cm������P��Qͬʱ�ӵ�A��������1cm/s���ٶȷֱ���A��B��C��A��D��C��·�����C�˶������˶�ʱ��Ϊx(��λ��s)���ı���PBDQ�����Ϊy(��λ��cm2)����y��x(0��x��8)֮��ĺ�����ϵ������ͼ���ʾΪ( )
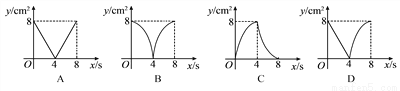
A. ��A�� B. ��B�� C. ��C�� D. ��D��
 B
���������������������������ͼ�Σ���������ۣ�
��0��x��4ʱ�������ı���PBDQ�����=��ABD���������APQ��������г�������ϵʽ���Ӷ��õ�����ͼ��
��4��x��8ʱ�������ı���PBDQ�����=��BCD���������CPQ��������г�������ϵʽ���Ӷ��õ�����ͼ���ٽ���ĸ�ѡ��ɵý⣮
��������
��0��x��4ʱ��
�������εı߳�Ϊ4cm��
��y=S��...
B
���������������������������ͼ�Σ���������ۣ�
��0��x��4ʱ�������ı���PBDQ�����=��ABD���������APQ��������г�������ϵʽ���Ӷ��õ�����ͼ��
��4��x��8ʱ�������ı���PBDQ�����=��BCD���������CPQ��������г�������ϵʽ���Ӷ��õ�����ͼ���ٽ���ĸ�ѡ��ɵý⣮
��������
��0��x��4ʱ��
�������εı߳�Ϊ4cm��
��y=S��...
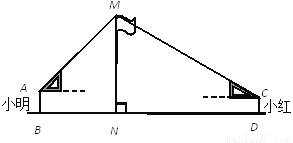
��ͼ���ڻ���ϣ�С����С�������һ�����ǰ�������ѧУ��˸߶ȣ���֪С�����۾������ľ��루AB����1.7m���������Լ���λ�ã��跨ʹ�����ǰ��һ��ֱ�DZ߱���ˮƽ����б������˶���M��ͬһ��ֱ���ϣ������˶���M����Ϊ45�㣻С����۾������ľ��루CD����1.5m����ͬ���ķ��������˶���M������Ϊ30�㣮�������28����λ��������ࣨ��B��N��D��ͬһ��ֱ���ϣ���������MN�ĸ߶ȣ����ο����ݣ�  �����������������
�����������������
 ��˸�ԼΪ12�ף�
���������������������A��AE��MN��E������C��CF��MN��F����EF=0.2m���ɡ�AEM�ǵ���ֱ�������εó�AE=ME����AE=ME=xm����MF=(x+0.2)m��FC=(28-x)m����Rt��MFC�У���MF=CF•tan��MCF���ⷽ�����x��ֵ����MN=ME+EN��
��������� ����A��AE��MN��E��
����C��CF��MN��F
��EF= =...
��˸�ԼΪ12�ף�
���������������������A��AE��MN��E������C��CF��MN��F����EF=0.2m���ɡ�AEM�ǵ���ֱ�������εó�AE=ME����AE=ME=xm����MF=(x+0.2)m��FC=(28-x)m����Rt��MFC�У���MF=CF•tan��MCF���ⷽ�����x��ֵ����MN=ME+EN��
��������� ����A��AE��MN��E��
����C��CF��MN��F
��EF= =... ֱ��y=3x-3��������y=x2 ��x+1�Ľ���ĸ�����________ .
 1
����������������
����ֱ��y=3x��3��������y=x2��x+1�н��㣬��3x��3=x2��x+1��x2��4x+4=0���ߡ�=16��16=0�������������ȵ�ʵ��������ֱ��y=3x��3��������y=x2��x+1��1�����㣮
�ʴ�Ϊ��1��
1
����������������
����ֱ��y=3x��3��������y=x2��x+1�н��㣬��3x��3=x2��x+1��x2��4x+4=0���ߡ�=16��16=0�������������ȵ�ʵ��������ֱ��y=3x��3��������y=x2��x+1��1�����㣮
�ʴ�Ϊ��1�� ��֪����y��mx2��6x��1(m�dz���)��
(1)��֤������mΪ��ֵ���ú�����ͼ����y���ϵ�һ�����㣻
(2)���ú�����ͼ����x��ֻ��һ�����㣬��m��ֵ��
 ��1��֤������������2��m��ֵΪ0��9.
�������������������1�����ݽ���ʽ��֪����x=0ʱ����mֵ�أ��ʿ�֪����mΪ��ֵ������y= ��6x+1��ͼ����y����һ�����㣨0��1����
��2��Ӧ������������ۣ��ٵ�����Ϊһ�κ���ʱ����x����һ�����㣻
�ڵ�����Ϊ���κ���ʱ�����ø���ϵ���Ĺ�ϵ���
�����������1����x=0ʱ��y=1��
���Բ���mΪ��ֵ������y= ��6...
��1��֤������������2��m��ֵΪ0��9.
�������������������1�����ݽ���ʽ��֪����x=0ʱ����mֵ�أ��ʿ�֪����mΪ��ֵ������y= ��6x+1��ͼ����y����һ�����㣨0��1����
��2��Ӧ������������ۣ��ٵ�����Ϊһ�κ���ʱ����x����һ�����㣻
�ڵ�����Ϊ���κ���ʱ�����ø���ϵ���Ĺ�ϵ���
�����������1����x=0ʱ��y=1��
���Բ���mΪ��ֵ������y= ��6... С����ɲ������s(m)���ٶ�v(km/h)֮��ĺ�����ϵʽΪs��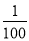 v2��һ��С�����ٶ�Ϊ100km/h����ǰ��80m��ͣ��һ�����ϳ�����ʱɲ��_______(��ᡱ���ᡱ)��Σ�գ�
v2��һ��С�����ٶ�Ϊ100km/h����ǰ��80m��ͣ��һ�����ϳ�����ʱɲ��_______(��ᡱ���ᡱ)��Σ�գ�
 ��
�����������������������Ѵ��뼴�����s��ֵ����80�Ƚϼ����ж�.
���У���ʱ��
���ʱɲ������Σ��.
��
�����������������������Ѵ��뼴�����s��ֵ����80�Ƚϼ����ж�.
���У���ʱ��
���ʱɲ������Σ��. ��֪������y��x2��2x��m��1��x����������ͬ�Ľ��㣬����y�� �Ĵ���ͼ����( )
�Ĵ���ͼ����( )

A. ��A�� B. ��B�� C. ��C�� D. ��D��
 A
��������������y=x2-2x+m+1��x����������ͬ�Ľ��㣬�ɵá�=��-2��2-4��m+1����0�����m��0����˿ɵú���y=��ͼ��λ�ڶ��������ޣ�
��ѡ��A��
A
��������������y=x2-2x+m+1��x����������ͬ�Ľ��㣬�ɵá�=��-2��2-4��m+1����0�����m��0����˿ɵú���y=��ͼ��λ�ڶ��������ޣ�
��ѡ��A�� ��ͼ�����ij��б��AB�ij���Ϊ10�ף��Ҹ�б����ߵ�A������BC��Ǧ���߶�Ϊ8�ף����б�µ��±�
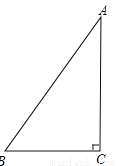
 ��������������������ȸ���AB��AC�ij����Լ����ɶ����ó�BC�ij��ȣ��������±ȵļ��㷨��ó��𰸣�
�����������ij��б��AB�ij���Ϊ10�ף��Ҹ�б����ߵ�A������BC��Ǧ���߶�Ϊ8�ף�
��ˮƽ����BC= =6��m����
���б�µ��±��ǣ� ��
��������������������ȸ���AB��AC�ij����Լ����ɶ����ó�BC�ij��ȣ��������±ȵļ��㷨��ó��𰸣�
�����������ij��б��AB�ij���Ϊ10�ף��Ҹ�б����ߵ�A������BC��Ǧ���߶�Ϊ8�ף�
��ˮƽ����BC= =6��m����
���б�µ��±��ǣ� �� ��ͼ��һ��С���ɵ��������¶�i=1��2����������ǰ����10 m����ʱС��������ĸ߶�Ϊ( )��
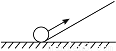
A��5m B��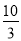 m C��4
m C��4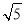 m D��2
m D��2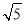 m
m
 D.
��������
���������������ͼ������������δ֪����ʾ��Ӧ���߶εij��ȣ������ù��ɶ����з�����⼴�ɣ�
�����������ͼ��
Rt��ABC��tanA=��AB=10��
��BC=x����AC=2x��
��x2+��2x��2=102��
��ã�����ֵ��ȥ����
����ʱС��������ĸ߶�Ϊ�ף�
��ѡD.
D.
��������
���������������ͼ������������δ֪����ʾ��Ӧ���߶εij��ȣ������ù��ɶ����з�����⼴�ɣ�
�����������ͼ��
Rt��ABC��tanA=��AB=10��
��BC=x����AC=2x��
��x2+��2x��2=102��
��ã�����ֵ��ȥ����
����ʱС��������ĸ߶�Ϊ�ף�
��ѡD. �������������ʵ�����ʽ��(1) �Cx-1=-��______��;(2)a-b+c=a-��______��
 x+1 b-c
�����������������ŷ���ɵã�(1) �Cx-1=-��x+1����(2)a-b+c=a-��b-c��.
x+1 b-c
�����������������ŷ���ɵã�(1) �Cx-1=-��x+1����(2)a-b+c=a-��b-c��. 
