题目内容
周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是()m

A. 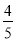 B.
B. 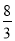 C. 4 D.
C. 4 D. 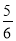
 B
【解析】设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是m²,故选B.
B
【解析】设窗户的宽是x,根据题意得
S=
=
∴当窗户宽是m时,面积最大是m²,故选B.
已知M、N是线段AB的垂直平分线上任意两点,则∠MAN和∠MBN之间关系是____.
 ∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置,
∴可能有以下四种情况:
①如图①,点M、N在线段AB两侧时,
∵M、N是线段AB的垂直平分线上任意两点,
∴点A、B两点关于直线MN轴对称,
∴线段MA、MB两点关于直线MN轴对称,
同理线段NA、NB两点关于直线MN轴对称,
∴△MAN与△MBN关于直线MN轴对称,
∴...
∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置,
∴可能有以下四种情况:
①如图①,点M、N在线段AB两侧时,
∵M、N是线段AB的垂直平分线上任意两点,
∴点A、B两点关于直线MN轴对称,
∴线段MA、MB两点关于直线MN轴对称,
同理线段NA、NB两点关于直线MN轴对称,
∴△MAN与△MBN关于直线MN轴对称,
∴... 如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: 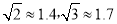 ,结果保留整数.)
,结果保留整数.)
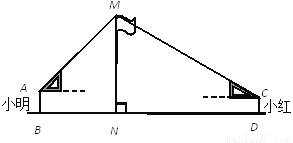
 旗杆高约为12米.
【解析】试题分析:过点A作AE⊥MN于E,过点C作CF⊥MN于F,则EF=0.2m.由△AEM是等腰直角三角形得出AE=ME,设AE=ME=xm,则MF=(x+0.2)m,FC=(28-x)m.在Rt△MFC中,由MF=CF•tan∠MCF,解方程求出x的值,则MN=ME+EN.
试题解析: 过点A作AE⊥MN于E,
过点C作CF⊥MN于F
则EF= =...
旗杆高约为12米.
【解析】试题分析:过点A作AE⊥MN于E,过点C作CF⊥MN于F,则EF=0.2m.由△AEM是等腰直角三角形得出AE=ME,设AE=ME=xm,则MF=(x+0.2)m,FC=(28-x)m.在Rt△MFC中,由MF=CF•tan∠MCF,解方程求出x的值,则MN=ME+EN.
试题解析: 过点A作AE⊥MN于E,
过点C作CF⊥MN于F
则EF= =... 如图,在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小芳距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
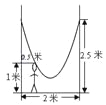
 0.5
【解析】试题分析:首先以点名所在的直线为x轴,最低点所在的直线为y轴建立平面直角坐标系,然后求出二次函数的解析式,最后计算出顶点坐标,顶点坐标的纵坐标就是距离地面的距离.
0.5
【解析】试题分析:首先以点名所在的直线为x轴,最低点所在的直线为y轴建立平面直角坐标系,然后求出二次函数的解析式,最后计算出顶点坐标,顶点坐标的纵坐标就是距离地面的距离. 如图,正方形ABCD的边长为1,E、F分别是边BC和CD上的动点(不与正方形的顶点重合),不管E、F怎样动,始终保持AE⊥EF.设BE=x,DF=y,则y是x的函数,函数关系式是( )
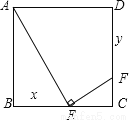
A. y=x+1 B. y=x-1 C. y=x2-x+1 D. y=x2-x-1
 C
【解析】试题分析:易证△ABE∽△ECF,根据相似三角形对应边的比相等即可求解.
【解析】
∵∠BAE和∠EFC都是∠AEB的余角.
∴∠BAE=∠FEC.
∴△ABE∽△ECF
那么AB:EC=BE:CF,
∵AB=1,BE=x,EC=1﹣x,CF=1﹣y.
∴AB•CF=EC•BE,
即1×(1﹣y)=(1﹣x)x.
化简得:y=x2...
C
【解析】试题分析:易证△ABE∽△ECF,根据相似三角形对应边的比相等即可求解.
【解析】
∵∠BAE和∠EFC都是∠AEB的余角.
∴∠BAE=∠FEC.
∴△ABE∽△ECF
那么AB:EC=BE:CF,
∵AB=1,BE=x,EC=1﹣x,CF=1﹣y.
∴AB•CF=EC•BE,
即1×(1﹣y)=(1﹣x)x.
化简得:y=x2... 如图所示,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对应的纵坐标如下.

(1)求A,B,C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(3)当矩形DEFG的面积S最大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
(4)若点D的坐标为(1,0),求矩形DEFG的面积.
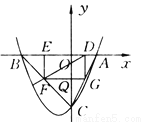
 (1)A(2,0),B(-4,0),C(0,-4);(2)S矩形DEFG=12m-6m2(0<m<2);(3)k的取值范围是k≠且k>0;(4)S矩形DEFG=6.
【解析】试题分析:(1)可任选三组坐标,用待定系数法即可求出抛物线P的解析式.然后根据抛物线P的解析式即可得出A、B、C三点的坐标;
(2)求矩形的面积需知道矩形的长和宽,可先在直角三角形AOC中,根据AD,OA,DG,C...
(1)A(2,0),B(-4,0),C(0,-4);(2)S矩形DEFG=12m-6m2(0<m<2);(3)k的取值范围是k≠且k>0;(4)S矩形DEFG=6.
【解析】试题分析:(1)可任选三组坐标,用待定系数法即可求出抛物线P的解析式.然后根据抛物线P的解析式即可得出A、B、C三点的坐标;
(2)求矩形的面积需知道矩形的长和宽,可先在直角三角形AOC中,根据AD,OA,DG,C... 直线y=3x-3与抛物线y=x2 -x+1的交点的个数是________ .
 1
【解析】【解析】
假设直线y=3x﹣3与抛物线y=x2﹣x+1有交点,则3x﹣3=x2﹣x+1,x2﹣4x+4=0,∵△=16﹣16=0,∴方程有两个相等的实数根,∴直线y=3x﹣3与抛物线y=x2﹣x+1有1个交点.
故答案为:1.
1
【解析】【解析】
假设直线y=3x﹣3与抛物线y=x2﹣x+1有交点,则3x﹣3=x2﹣x+1,x2﹣4x+4=0,∵△=16﹣16=0,∴方程有两个相等的实数根,∴直线y=3x﹣3与抛物线y=x2﹣x+1有1个交点.
故答案为:1. 已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
 (1)证明见解析;(2)m的值为0或9.
【解析】试题分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y= ﹣6x+1的图象都经过y轴上一个定点(0,1).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
试题解析:(1)当x=0时,y=1.
所以不论m为何值,函数y= ﹣6...
(1)证明见解析;(2)m的值为0或9.
【解析】试题分析:(1)根据解析式可知,当x=0时,与m值无关,故可知不论m为何值,函数y= ﹣6x+1的图象都经过y轴上一个定点(0,1).
(2)应分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用根与系数的关系解答.
试题解析:(1)当x=0时,y=1.
所以不论m为何值,函数y= ﹣6... 如图,一个小球由地面沿着坡度i=1∶2的坡面向上前进了10 m,此时小球距离地面的高度为( ).
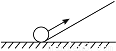
A.5m B.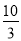 m C.4
m C.4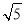 m D.2
m D.2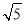 m
m
 D.
【解析】
试题分析:画出草图,根据题意用未知数表示相应的线段的长度,再运用勾股定理列方程求解即可.
试题解析:如图:
Rt△ABC中,tanA=,AB=10.
设BC=x,则AC=2x,
∴x2+(2x)2=102,
解得,(负值舍去).
即此时小球距离地面的高度为米.
故选D.
D.
【解析】
试题分析:画出草图,根据题意用未知数表示相应的线段的长度,再运用勾股定理列方程求解即可.
试题解析:如图:
Rt△ABC中,tanA=,AB=10.
设BC=x,则AC=2x,
∴x2+(2x)2=102,
解得,(负值舍去).
即此时小球距离地面的高度为米.
故选D. 
