题目内容
2.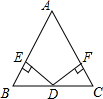 已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.
已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.
分析 首先运用HL定理证明△BDE≌△CDF,进而得到∠B=∠C,运用等腰三角形的判定定理即可解决问题.
解答  证明:如图,
证明:如图,
∵D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,
∴BD=CD,△BDE、△CDF均为直角三角形;
在△BDE、△CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$,
∴△BDE≌△CDF(HL),
∴∠B=∠C,
∴AB=AC.
点评 该题主要考查了全等三角形的判定、等腰三角形的判定等几何知识点及其应用问题;牢固掌握全等三角形的判定、等腰三角形的判定等几何知识点是解题的基础和关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
13.为了实现医药卫生改革的目标,经初步测算,2011-2015年各级政府一共需要投入人民币8500亿元,这个数据用科学记数法可表示为( )
| A. | 8.5×1012元 | B. | 8.5×1010元 | C. | 0.85×1012元 | D. | 8.5×1011元 |
14.已知一次函数y=kx+b,k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
11.⊙O的内接正三角形的边长等于3$\sqrt{3}$,则⊙O的面积等于( )
| A. | 27π | B. | $\frac{27}{4}$π | C. | 9π | D. | $\frac{9}{4}$π |
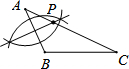
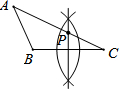
 如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC=AC,则下列选项中,一定符合要求的作图痕迹是( )
如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC=AC,则下列选项中,一定符合要求的作图痕迹是( )

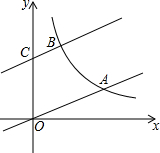 如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.
如图,直线y=$\frac{1}{3}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{3}$x向上平移3个单位得到直线y=ax+b,它与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B.若OA=2BC.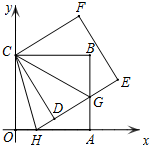 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形OCBA绕点C逆时针旋转角度一个锐角度数α,得到正方形DCFE,ED交线段AB与点G,ED的延长线交线段OA于点H,连CH、CG.