题目内容
11.⊙O的内接正三角形的边长等于3$\sqrt{3}$,则⊙O的面积等于( )| A. | 27π | B. | $\frac{27}{4}$π | C. | 9π | D. | $\frac{9}{4}$π |
分析 根据题意画出图形,连接OB,作OD⊥BC,由垂径定理可得到BD=$\frac{1}{2}$BC,再由等边三角形的性质可得到∠OBD的度数,由特殊角的三角函数值即可求出r的值,进而得出⊙O的面积.
解答  解:如图所示,连接OB,作OD⊥BC.
解:如图所示,连接OB,作OD⊥BC.
∵BC=3$\sqrt{3}$,
∴BD=$\frac{1}{2}$BC=$\frac{3\sqrt{3}}{2}$.
∵△ABC是等边三角形,
∴∠OBD=30°,
∴OB=$\frac{BD}{cos30°}$=$\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$=3,
∴S⊙O=π×32=9π.
故选C.
点评 本题考查的是正多边形和圆及特殊角的三角函数值、垂径定理,根据题意画出图形利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
1.国家体育场位于北京奥林匹克公园中心区南部,为2008年北京奥运会的主体育场.国家体育场“鸟巢”建筑面积达258000平方米,场内观众坐席约为91000个,举行了奥运会、残奥会开闭幕式、田径比赛及足球比赛决赛.用科学记数法表示258000应为( )
| A. | 2.58×103 | B. | 25.8×104 | C. | 2.58×105 | D. | 258×103 |
20.设a,b为实数,且a<b,则下列不等式变形正确的是( )
| A. | 3a<3b | B. | -a<-b | C. | a+1>b+1 | D. | $\frac{a}{2}>\frac{b}{2}$ |
1.下列各组数为勾股数的是( )
| A. | 6,12,13 | B. | 3,4,7 | C. | 8,15,16 | D. | 5,12,13 |
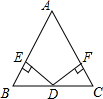 已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.
已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.