题目内容
14.已知一次函数y=kx+b,k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 首先根据一次函数的图象经过的象限确定k、b的符号,然后分别确定k为负数的概率和b为负数的概率,从而确定同为负数即一次函数的图象经过二、三、四象限的概率.
解答 解:当y=kx+b的图象经过二、三、四象限时k<0,b<0,
∵k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,
∴k为负数的概率为$\frac{1}{2}$,b为负数的概率为$\frac{2}{3}$,
∴该一次函数的图象经过二、三、四象限的概率为$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{3}$,
故选A.
点评 考查了一次函数的图象与系数的关系及概率公式的知识,经过二三四象限的一次函数的k<0,b<0.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
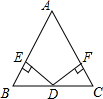 已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.
已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.