��Ŀ����
10��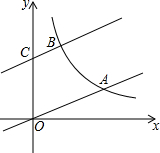 ��ͼ��ֱ��y=$\frac{1}{3}$x��˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��y=$\frac{1}{3}$x����ƽ��3����λ�õ�ֱ��y=ax+b������y�ύ�ڵ�C����˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�B����OA=2BC��
��ͼ��ֱ��y=$\frac{1}{3}$x��˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��y=$\frac{1}{3}$x����ƽ��3����λ�õ�ֱ��y=ax+b������y�ύ�ڵ�C����˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�B����OA=2BC����1����˫����y=$\frac{k}{x}$�ı���ʽ��
��2������ͼ��ֱ��д��ax+b-$\frac{k}{x}$��0ʱx��ȡֵ��Χ��
���� ��1���ֱ����A��B��AD��x�ᣬBE��x�ᣬCF��BE�ڵ�F������A��2x��$\frac{2}{3}$x��������OA=3BC���ʿɵó�B��x��$\frac{1}{3}$x+3�����ٸ��ݷ�����������k=xyΪ��ֵ���k��ֵ���ɣ�
��2���������̣���ý���B�����꣬����ͼ�����ax+b-$\frac{k}{x}$��0ʱx��ȡֵ��Χ��
��� �⣺��1���ֱ����A��B��AD��x�ᣬBE��x�ᣬCF��BE�ڵ�F����A��2x��$\frac{2}{3}$x����
��OA=2BC��BC��OA��CF��x�ᣬ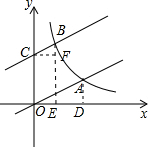
���BCF�ס�AOD��
��CF=$\frac{1}{2}$OD��
�ߵ�B��ֱ��y=$\frac{1}{3}$x+3�ϣ�
��B��x��$\frac{1}{3}$x+3����
�ߵ�A��B��˫����y=$\frac{k}{x}$��k��0��x��0���ϣ�
��2x•$\frac{2}{3}$x=x•��$\frac{1}{3}$x+3�������x=3��
��k=2��3��$\frac{2}{3}$��3=12��
��˫���ߵı���ʽΪy=$\frac{12}{x}$��
��2����$\left\{\begin{array}{l}{y=\frac{1}{3}x+3}\\{y=\frac{12}{x}}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$��
��B��3��4����
��ax+b-$\frac{k}{x}$��0ʱx��ȡֵ��Χ��0��x��3��
���� ���⿼����Ƿ�����������һ�κ����Ľ��㣬�����������������ߣ����A��B��������꣬�ٸ���k=xy���ص��г������DZ���Ĺؼ���

| A�� | 2.58��103 | B�� | 25.8��104 | C�� | 2.58��105 | D�� | 258��103 |
������ֱ�߱�������ֱ�����أ�ͬλ�����
�ڹ�һ������ֻ��һ��ֱ������ֱ֪�ߴ�ֱ
�������������Ļ�һ����������
��-$\sqrt{8}$��$\root{3}{-27}$��
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | 3a��3b | B�� | -a��-b | C�� | a+1��b+1 | D�� | $\frac{a}{2}��\frac{b}{2}$ |
 ��ͼ����ABC�У���1=��2����3=��4��EF��BC��˵��BE+CF=EF��
��ͼ����ABC�У���1=��2����3=��4��EF��BC��˵��BE+CF=EF��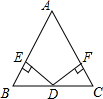 ��֪����ͼ��D�ǡ�ABC��BC�ߵ��е㣬DE��AB��DF��AC������ֱ�ΪE��F����DE=DF����֤��AB=AC��
��֪����ͼ��D�ǡ�ABC��BC�ߵ��е㣬DE��AB��DF��AC������ֱ�ΪE��F����DE=DF����֤��AB=AC��