题目内容
17．因式分解：（1）m（a2+b2）+n（a2+b2）；
（2）18（a-b）3-12b（b-a）2；
（3）（2a+b）（2a-3b）-3a（2a+b）；
（4）x（x+y）（x-y）-x（x+y）2．
分析 （1）直接提取公因式（a2+b2）得出即可；
（2）直接提取公因式6（a-b）2得出即可；
（3）直接提取公因式（2a+b）得出即可；
（4）直接提取公因式x（x+y）得出即可．
解答 解：（1）m（a2+b2）+n（a2+b2）
=（a2+b2）（m+n）；
（2）18（a-b）3-12b（b-a）2；
=6（a-b）2[3（a-b）+2b）]
=6（a-b）2（3a-b）；
（3）（2a+b）（2a-3b）-3a（2a+b）
=（2a+b）（2a-3b-3a）
=-（2a+b）（a+3b）；
（4）x（x+y）（x-y）-x（x+y）2
=x（x+y）[x-y-（x+y）]
=-2yx（x+y）．
点评 此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
练习册系列答案
相关题目
7．如图所示，是一列用若干火柴棒摆成的由正三角形组成的图案：
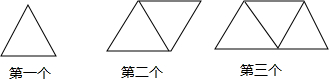
（1）完成下表的填空
（2）某同学用若干火柴棒按如上图所列的方式摆图案，摆完了第1个后，摆第2个，按着摆第3个，…，摆完第n个后剩下22根火柴棒，当他摆完第n+1个图案还多1根，问最后摆的图案是第几个图案？
（1）完成下表的填空
| 正三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |
8．
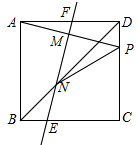如图，正方形ABCD中，点P为CD上一点，线段AP的垂直平分线MN交BD于点N，点M为垂足，交两边于点E、F，连接PN，则下列结论，其中正确的有（ ）
①∠DNP=∠DAP；
②PC=$\sqrt{2}$BN；
③$\frac{DP+DC}{DN}$为常数；
④MN=MF+NE．
如图，正方形ABCD中，点P为CD上一点，线段AP的垂直平分线MN交BD于点N，点M为垂足，交两边于点E、F，连接PN，则下列结论，其中正确的有（ ）①∠DNP=∠DAP；
②PC=$\sqrt{2}$BN；
③$\frac{DP+DC}{DN}$为常数；
④MN=MF+NE．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
6．已知一次函数y=-x+1与反比例函数y=-$\frac{2}{x}$，x，y一些对应值如表：
那么不等式-x+1＜-$\frac{2}{x}$（x＜0）的解为-1＜x＜0．
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=-x+1 | … | 4 | 3 | 2 | 0 | -1 | -2 | … |
| y=-$\frac{2}{x}$ | … | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ | … |