题目内容
已知点A（m，n）在抛物线y=x2+bx+c上，且n＜0，求证：抛物线和x轴有两个交点．
考点：抛物线与x轴的交点
专题：证明题
分析：根据抛物线的开口方向和点A的位置可以证得结论．
解答：
证明：∵抛物线的解析式y=x2+bx+c的二次项系数是1，1＞0，
∴抛物线开口方向向上．
又∵点A（m，n）在抛物线y=x2+bx+c上，且n＜0，
∴该抛物线的顶点坐标位于x轴以下，
∴抛物线和x轴有两个交点．
证明：∵抛物线的解析式y=x2+bx+c的二次项系数是1，1＞0，∴抛物线开口方向向上．
又∵点A（m，n）在抛物线y=x2+bx+c上，且n＜0，
∴该抛物线的顶点坐标位于x轴以下，
∴抛物线和x轴有两个交点．
点评：本题考查了抛物线与x轴的交点．解题时，需要熟悉抛物线的性质．
练习册系列答案
相关题目
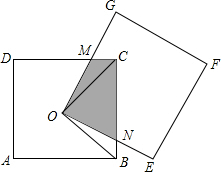如图，正方形ABCD和正方形OEFG的边长均为4，O为正方形ABCD的中心．连接OG、OE分别与CD、BC交于M、N点，连接OC、OB．
如图，在四边形ABCD中，AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线，且BE∥FD，AH∥CG，证明四边形ABCD为平行四边形．
如图，在△ABC中，点D在BC边上．