题目内容
 如图,在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,且BE∥FD,AH∥CG,证明四边形ABCD为平行四边形.
如图,在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,且BE∥FD,AH∥CG,证明四边形ABCD为平行四边形.考点:平行四边形的判定
专题:证明题
分析:由BE∥FD,AH∥CG,在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,易得∠ABC+∠BCD=∠BAD+∠ADC=180°,则可证得AB∥CD,同理可得AD∥BC,则可证得四边形ABCD为平行四边形.
解答: 证明:∵BE∥FD,AH∥CG,
证明:∵BE∥FD,AH∥CG,
∴∠2=∠3,∠5=∠6,
∵∠1+∠2=∠3+∠4,
∴∠4+∠6=∠1+∠3,
∵在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,
∴∠1=
∠ABC,∠3=
∠BCD,∠4=
∠BAD,∠6=
∠ADC,
∴∠ABC+∠BCD=∠BAD+∠ADC=180°,
∴AB∥CD,
同理:AD∥BC,
∴四边形ABCD为平行四边形.
 证明:∵BE∥FD,AH∥CG,
证明:∵BE∥FD,AH∥CG,∴∠2=∠3,∠5=∠6,
∵∠1+∠2=∠3+∠4,
∴∠4+∠6=∠1+∠3,
∵在四边形ABCD中,AH、CG、BE、FD分别是∠A、∠C、∠B、∠D的角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC+∠BCD=∠BAD+∠ADC=180°,
∴AB∥CD,
同理:AD∥BC,
∴四边形ABCD为平行四边形.
点评:此题考查了平行四边形的判定.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
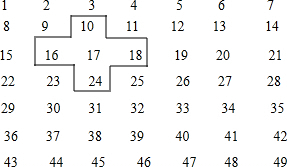 如图是一张按一定顺序排列的自然数表,用一个有五个空格的十字框可以框出五个数字,现框出的五个数字中,四个角上的数字分别是10、16、18、24.如果框出的四个角上的四个数字之和为132,那么,被框出的五个数字分别是
如图是一张按一定顺序排列的自然数表,用一个有五个空格的十字框可以框出五个数字,现框出的五个数字中,四个角上的数字分别是10、16、18、24.如果框出的四个角上的四个数字之和为132,那么,被框出的五个数字分别是