题目内容
 如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上的一动点,DE⊥BC,DF⊥AC,垂足为E、F,当线段EF的长最小时,cos∠EFD=
如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上的一动点,DE⊥BC,DF⊥AC,垂足为E、F,当线段EF的长最小时,cos∠EFD=考点:矩形的判定与性质,垂线段最短,锐角三角函数的定义
专题:
分析:连接CD,判断出四边形CEDF是矩形,再根据矩形的对角线相等可得EF=CD,然后根据垂线段最短可得CD⊥AB时线段EF的长最小,利用勾股定理列式求出AB,根据矩形的性质可得∠EFD=∠ECD,再根据同角的余角相等求出∠ECD=∠A,从而得到∠EFD=∠A,然后根据锐角三角函数的定义列式计算即可得解.
解答: 解:如图,连接CD,
解:如图,连接CD,
∵DE⊥BC,DF⊥AC,∠ACB=90°,
∴四边形CEDF是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时线段EF的长最小,
∵AC=3,BC=4,
∴AB=
=
=5,
∵四边形CEDF是矩形,
∴∠EFD=∠ECD,
∵∠ECD+∠ACD=90°,
∠A+∠ACD=90°,
∴∠ECD=∠A,
∴∠EFD=∠A,
在Rt△ABC中,cos∠A=
=
,
∴cos∠EFD=cos∠A=
.
故答案为:
.
 解:如图,连接CD,
解:如图,连接CD,∵DE⊥BC,DF⊥AC,∠ACB=90°,
∴四边形CEDF是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时线段EF的长最小,
∵AC=3,BC=4,
∴AB=
| AC2+BC2 |
| 32+42 |
∵四边形CEDF是矩形,
∴∠EFD=∠ECD,
∵∠ECD+∠ACD=90°,
∠A+∠ACD=90°,
∴∠ECD=∠A,
∴∠EFD=∠A,
在Rt△ABC中,cos∠A=
| AC |
| AB |
| 3 |
| 5 |
∴cos∠EFD=cos∠A=
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查了矩形的判定与性质,垂线段最短的性质,锐角三角函数的定义,熟记性质与判定方法并确定出EF最短时的位置是解题的关键.

练习册系列答案
相关题目
若
与1互为相反数,则x等于( )
| 2 |
| x-1 |
| A、-1 | B、1 | C、2 | D、3 |
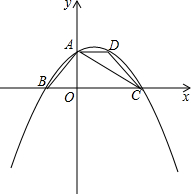 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2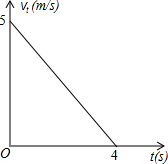 一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据:
一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据: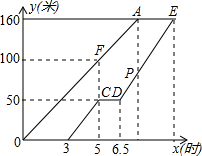 如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为
如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为