Question

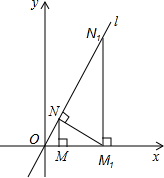如图，已知直线l：y=

3

x，过点M（1，0）作x轴的垂线交直线l于点N，过点N作直线l的垂线交x轴于点M₁；过点M₁作x轴的垂线交直线l于N₁，过点N₁作直线l的垂线交x轴于点M₂，…；按此作法继续下去，则点M₅的坐标为

 

．

Answer 1

考点：一次函数图象上点的坐标特征

专题：规律型

分析：本题需先求出OM₁和OM₂的长，再根据题意得出OM_n=4ⁿ，求出OM₄的长等于4⁴，即可求出M₅的坐标．

解答：解：∵直线l的解析式是y=

3

x，
∴∠NOM=60°，∠ONM=30°．
∵点M的坐标是（2，0），NM∥y轴，点N在直线y=

3

x上，
∴NM=2

3

，
∴ON=2OM=4．
又∵NM₁⊥l，即∠ONM₁=90°
∴OM₁=2ON=4¹OM=8．
同理，OM₂=4OM₁=4²OM，
OM₃=4OM₂=4×4²OM=4³OM，
…
OM₅=4⁵OM=1024．
∴点M₅的坐标是（2048，0）．
故答案是：（2048，0）．

点评：本题主要考查一次函数图象上点的坐标特点，涉及到如何根据一次的解析式和点的坐标求线段的长度，以及如何根据线段的长度求出点的坐标，解题时要注意相关知识的综合应用．