题目内容
 如图,平面直角坐标系中有依次向右排列的菱形A1B1C1A2、A2B2C2A3、A3B3C3A4…,其中点A1、A2、A3…均在x轴正半轴上,点A1和A2的坐标分别为(1,0)和(2,0),∠B1A1A2=∠B2A2A3=∠B3A3A4=…=60°,点B1、B2、B3…都在第一象限,且位于同一条过原点的直线上,则这条直线的解析式是
如图,平面直角坐标系中有依次向右排列的菱形A1B1C1A2、A2B2C2A3、A3B3C3A4…,其中点A1、A2、A3…均在x轴正半轴上,点A1和A2的坐标分别为(1,0)和(2,0),∠B1A1A2=∠B2A2A3=∠B3A3A4=…=60°,点B1、B2、B3…都在第一象限,且位于同一条过原点的直线上,则这条直线的解析式是考点:菱形的性质,一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:规律型
分析:根据点A1和A2的坐标分别为(1,0)和(2,0)依次求出菱形的边长,进而求得B1 的坐标,根据B1 的坐标即可求得这条直线的解析式,根据菱形的边长求得A1、A2、A3…的坐标然后分别表示出C1、C2、C3…的坐标找出规律进而求得Cn的坐标
解答:解答:解:∵点A1和A2的坐标分别为(1,0)和(2,0),
∴A1A2=1,
∴A1B=11,
∵∠B1A1A2=∠B2A2A3=∠B3A3A4=…=60°,
∴B1的纵坐标为:sin∠A2A1B1•A1B1=sin60°•AB=
,横坐标为OA+cos60°•A1B1=1+
=
,
∴B1(
,
),
设直线OB1 的解析式为:y=kx,则
=
k,解得:k=
,
∴直线OB1 的解析式为:y=
x;
∵菱形A1B1C1A2、A2B2C2A3、A3B3C3A4…,
∴OA2=2OA1=2,OA3=2OA2=4,OA4=2OA3=8,…,
∴C1(
,
),C2(5,
),C3(10,2
),C4(20,4
)…,
∴Cn(
×2(n-1),
×2(n-1));
∴A1A2=1,
∴A1B=11,
∵∠B1A1A2=∠B2A2A3=∠B3A3A4=…=60°,
∴B1的纵坐标为:sin∠A2A1B1•A1B1=sin60°•AB=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴B1(
| 3 |
| 2 |
| ||
| 2 |
设直线OB1 的解析式为:y=kx,则
| ||
| 2 |
| 3 |
| 2 |
| ||
| 3 |
∴直线OB1 的解析式为:y=
| ||
| 3 |
∵菱形A1B1C1A2、A2B2C2A3、A3B3C3A4…,
∴OA2=2OA1=2,OA3=2OA2=4,OA4=2OA3=8,…,
∴C1(
| 5 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
∴Cn(
| 5 |
| 2 |
| ||
| 2 |
点评:点评:本题是对点的坐标变化规律的考查,主要利用了菱形的性质,解直角三角形,根据已知点的变化规律求出菱形的边长得出系列A点的坐标,得出系列C点的坐标,找出规律是解题的关键.

练习册系列答案
相关题目
函数y=(a+1)xa-1是正比例函数,则a的值是( )
| A、2 | B、-1 | C、2或-1 | D、-2 |
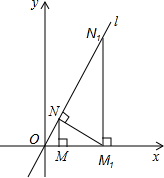 如图,已知直线l:
如图,已知直线l: 如图,OC⊥AB,OD⊥OE,图中与∠1与互余的角是
如图,OC⊥AB,OD⊥OE,图中与∠1与互余的角是 已知矩形纸片ABCD的边长AB=4cm,AD=2cm.将矩形纸片沿EF折叠,使点A与点C重合,如图,则线段EC的长为
已知矩形纸片ABCD的边长AB=4cm,AD=2cm.将矩形纸片沿EF折叠,使点A与点C重合,如图,则线段EC的长为